Пусть имеется одноканальная СМО с очередью, на которую не наложено никаких ограничений (ни по длине очереди, ни по времени ожидания). На эту СМО поступает поток заявок с интенсивностью 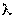 ; поток обслуживаний имеет интенсивность
; поток обслуживаний имеет интенсивность 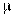 , обратную среднему времени обслуживания заявки tоб. Требуется найти финальные вероятности состояний СМО, а также характеристики ее эффективности:
, обратную среднему времени обслуживания заявки tоб. Требуется найти финальные вероятности состояний СМО, а также характеристики ее эффективности:
Lсист- среднее число заявок в системе;
Wсист- среднее время пребывания заявки в системе;
Lоч- среднее число заявок в очереди;
Wоч- среднее время пребывания заявки в очереди;
Рзан- вероятность того, что канал занят (степень загрузки канала).
Что касается абсолютной пропускной способности А и относительной Q, то вычислять их нет надобности: в силу того, что очередь не ограничена, каждая заявка рано или поздно будет обслужена, поэтому А = 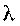 , по той же причине Q=1.
, по той же причине Q=1.
Решение. Состояния системы будем нумеровать по числу заявок, находящихся в СМО:
S0- канал свободен;
S1- канал занят, очереди нет;
S2- канал занят, одна заявка стоит в очереди; и т.д.
Теоретически число состояний ничем не ограничено. Граф состояний имеет вид
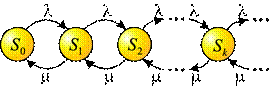
Это - схема гибели и размножения, но с бесконечным числом состояний. По всем стрелкам поток заявок с интенсивностью 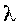 переводит систему слева направо, а справа налево - поток обслуживаний с интенсивностью
переводит систему слева направо, а справа налево - поток обслуживаний с интенсивностью 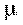 . Если
. Если 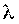 >
> 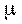 , то канал с заявками не справляется, очередь растет до бесконечности. Если
, то канал с заявками не справляется, очередь растет до бесконечности. Если 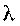 ≤
≤ 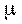 , то задача вполне разрешима.
, то задача вполне разрешима.
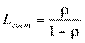
Теперь применим формулу Литтла и найдем среднее время пребывания заявки в системе:
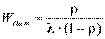
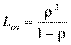
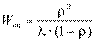
 2015-04-08
2015-04-08 1261
1261








