Пусть заказанная партия поступает с интенсивностью λ единиц в единицу времени. Очевидно, система может работать без дефицита, если интенсивность поставок λ превосходит интенсивность потребления v. Изменение уровня запаса для рассматриваемого случая изображено на рисунке 4.2.
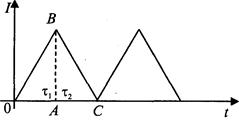
Рисунок 4.2 – Модель с конечной интенсивностью поступления заказа
В течение времени τ1 запас одновременно и поступает, и расходуется, это время накопления запаса. В течение τ2 запас только расходуется.
Таблица 4.2 – Показатели модели и формулы для их расчета
| № | Показатели модели | Формулы для расчета показателей модели |
| Длина цикла | 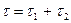 | |
| Максимальный наличный запас | 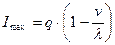 | |
| Издержки системы в единицу времени | 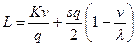 | |
| Величина оптимальной партии заказа | 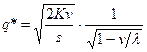 | |
| Оптимальный период возобновления заказа | 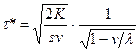 | |
| Составляющие оптимального периода возобновления заказа | 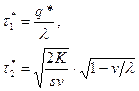 | |
| Минимальные издержки в единицу времени | 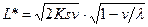 |
 2015-04-08
2015-04-08 864
864








