Проанализируем работу одноканальной СМО с ожиданием без ограничений на длину очереди и на время ожидания в очереди. Предполагаем, что входящий поток с интенсивностью λ и поток обслуживаний с интенсивностью μ простейшие. Длина очереди в данной СМО бесконечна, т.е. m → ∞. При условии, что λ < μ, т.е. ρ < 1, с течением времени устанавливается предельный режим и предельные вероятности состояний СМО существуют.
Характеристики данной СМО представлены в таблице 5.2.
Таблица 5.2– Предельные характеристики эффективности функционирования одноканальной СМО с ожиданием
| № | Предельные характеристики | Обозначения, формулы |
| Среднее время обслуживания одной заявки | 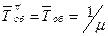
| |
| Показатель нагрузки (трафик) СМО | 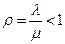
| |
| Вероятности состояний СМО | 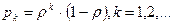
| |
| Вероятность отказа | 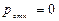
| |
| Вероятность того, что заявка будет принята в систему | 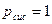
| |
| Относительная пропускная способность | 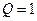
| |
| Абсолютная пропускная способность | 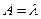
| |
| Интенсивность выходящего потока заявок | 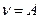
| |
| Среднее число заявок в очереди | 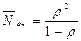
|
Продолжение таблицы 5.2
| № | Предельные характеристики | Обозначения, формулы |
| Среднее число заявок, находящихся под обслуживанием | 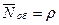
| |
| Среднее число заявок, находящихся в системе (как в очереди, так и под обслуживанием) | 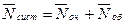
| |
| Среднее время ожидания заявки в очереди | 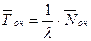
| |
| Среднее время пребывания заявки в системе (как в очереди, так и под обслуживанием) | 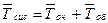
|
 2015-04-08
2015-04-08 505
505








