При простой случайной выборке отбор производится из всей массы единиц генеральной совокупности без предварительного расчленения ее на какие-либо группы, и единица совокупности совпадает с единицей наблюдения.
Различают простую случайную повторную выборку (после отбора какой-то единицы она снова возвращается в совокупность) и простую случайную бесповторную выборку (отобранная единица не возвращается в совокупность и вероятность попадания оставшихся единиц возрастает).
Поставим задачу определения параметров генеральной совокупности по результатам проведения простой случайной выборки.
Предварительно отметим, что в распределении величин выборочных средних и их отклонений наблюдаются определенные закономерности:
Ø Из возможных результатов простой случайной выборки наиболее вероятны такие, при которых величина выборочной средней будет близка к величине генеральной средней;
Ø При простой случайной выборке средняя арифметическая является несмещенной оценкой генеральной средней (несмещенная оценка-это оценка лишенная систематической ошибки);
Ø Чем больше обследуется единиц совокупности, тем меньше будет величина расхождений выборочных и генеральных характеристик;
Пусть генеральная совокупность представлена следующими условными показателями:
X1, X2,...,XN, где N – объем генеральной совокупности (число входящих в нее единиц).
Обозначим: xГ - среднее значение признака в генеральной совокупности (генеральная средняя); wГ – генеральная доля (доля единиц, обладающих данным значением признака в общем, числе единиц генеральной совокупности), например, доля числа бракованных единиц в общем количестве единиц в данной партии изделий;
SГ- среднее квадратическое отклонение в генеральной совокупности.
Произведем отбор простой случайной выборки (повторной или без повторной) объема n, причем n много меньше, чем N (n << N). Пусть эта выборка будет: X1, X2,...,X n
По этой выборке определим:
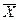 -среднее значение (выборочная средняя)
-среднее значение (выборочная средняя) 
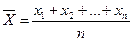 ;
;
w- выборочная доля (например, доля бракованных изделий в выборке);
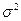 - выборочная дисперсия определится по формуле
- выборочная дисперсия определится по формуле 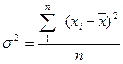 ;
;
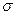 - среднее квадратическое отклонение в выборке.
- среднее квадратическое отклонение в выборке.
В математической статистике доказывается, что величина средней квадратической стандартной ошибки простой случайной выборки может быть определена следующими формулами:
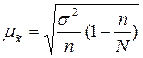
 для без повторной выборке;
для без повторной выборке;
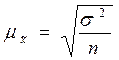 для повторной выборке.
для повторной выборке.
Среднюю стандартную ошибку выборочной доли определяют по следующим формулам;
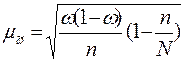 для без повторной выборке;
для без повторной выборке;
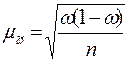 для повторной выборке.
для повторной выборке.
В тех случаях, когда объем генеральной совокупности N очень велик по сравнению с числом отобранных единиц n, величина 1 – 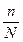 будет близка к единице, а потому его можно пренебречь.
будет близка к единице, а потому его можно пренебречь.
Выборочное наблюдение дает возможность определять насколько выборочная средняя (выборочная доля), может отличаться от генеральной средней (генеральной доли) в большую или меньшую сторону. Величина генеральной средней (генеральной доли) может быть представлена интервальной оценкой, для которых нижняя граница будет равна 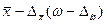 , а верхняя граница
, а верхняя граница 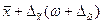 . Пределы, в которых с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительными, а вероятность p – доверительной вероятностью.
. Пределы, в которых с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительными, а вероятность p – доверительной вероятностью.
Величины 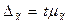 и
и 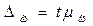 называются соответственно предельными ошибками выборочной средней и выборочной доли соответственно.
называются соответственно предельными ошибками выборочной средней и выборочной доли соответственно.
Видим, что предельная ошибка выборки равна t – кратному числу средних ошибок выборки.
Ниже приводится наиболее часто употредляемые уровни доверительной вепоятности (p=ф(t), ф(t) – функция Лапласса) и соответствующих значений t для выборок достаточно большого объема (n≥30):
| t | 1.96 | 2.00 | 2.58 | 3.00 | |
| Ф(t) | 0.683 | 0.950 | 0.954 | 0.990 | 0.997 |
Из последней графы следует, что вероятность появления ошибки, равной или большей утроенной средней ошибки выборки, т.е. 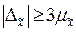 крайне мала и равна 0.003=(1-0.997). Такие маловероятные события считаются практически невозможными.
крайне мала и равна 0.003=(1-0.997). Такие маловероятные события считаются практически невозможными.
Доверительный интервал для генеральной средней будет иметь вид:
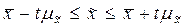
для генеральной доли:
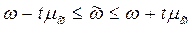
Пример. Для контроля качества поступившей партии зерна произведено 6%-ное выборочное обследование. В результате анализа установлено следующее распределение полученных методом выборки данных о влажности зерна:
Таблица 3.1
| Процент влажности (xi) | Число проб (fi) |
| до 8 | |
| 8-10 | |
| 10-12 | |
| 12-14 | |
| 14-16 | |
| 1 6 и выше | |
| Итого |
При условии, что к нестандартной продукции относятся образцы с влажностью от 16% и выше, установить для всей партии зерна:
1) с вероятностью 0,997 возможные пределы доли стандартной продукции;
2) с вероятностью 0,954 возможные пределы среднего процента влажности для всей партии зерна.
Решение: За величины открытых интервалов (у которых верхняя или нижняя границы точно не определены) условно примем величины смежного закрытого интервала. Т.е. величина первого интервала равна величине второго интервала и равно 2, а величина 6-го интервала равна величине 5-го и равна 2.
Следовательно, нижняя граница выборки равна хmin =8-2 = 6; верхняя граница выборки равна xmax =16+ 2=18.
Найдем среднее значение признака по формуле:
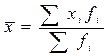 ,
, 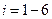
xi - значение признака на интервале (середина интервала);
fi - частота повторения признака на интервале
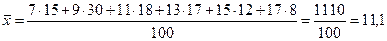 %
%
Найдем дисперсию признака по формуле:
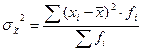
где 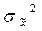 - дисперсия признака.
- дисперсия признака.
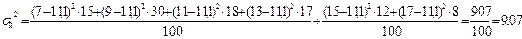
Среднее квадратичное отклонение 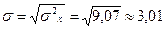
Коэффициент вариации 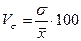 %=
%= 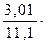 100%=27,13%
100%=27,13%
Коэффициент вариации меньше 33%, значит выборка однородная.
Возможные пределы удельного веса стандартной продукции для генеральной совокупности вероятностью 0,997 найдем из формулы:
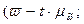
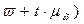
где 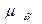 -средняя ошибка выборочной доли. Она находится по формуле:
-средняя ошибка выборочной доли. Она находится по формуле:
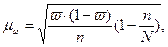
где N - общее число изделий в генеральной совокупности;
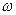 - частота появления альтернативного признака, равная m/n, где m - число случаев в выборке, когда продукция стандартная.
- частота появления альтернативного признака, равная m/n, где m - число случаев в выборке, когда продукция стандартная.
В нашем случае m = 100 - 8 = 92 и 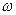 = 92 /100 = 0,92, а n / N = 0,06 т.к. проводилось 6%-ое обследование продукции. Тогда:
= 92 /100 = 0,92, а n / N = 0,06 т.к. проводилось 6%-ое обследование продукции. Тогда:
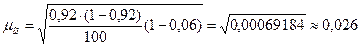
t: (0,997; 100) - 3, следовательно интервал равен:
(0,92 - 0,026 * 3; 0,92 + 0,026 * 3); (0,842; 0,998)
Т.е. с вероятностью 0,997 можно предполагать что в поступившей партии зерна доля стандартной находится в пределах от 84,2% до 99,8%.
Возможные пределы, в которых ожидается средний процент влажности всей поступившей партии зерна с вероятностью 0,954 найдем из формулы:
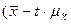 ;
; 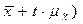
где t - коэффициент доверия при заданной степени вероятности (находится по таблице).
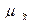 - средняя ошибка выборочной средней.
- средняя ошибка выборочной средней.
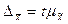 - предельная ошибка выборки.
- предельная ошибка выборки.
Средняя ошибка выборочной средней находится по формуле:
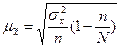 ,
,
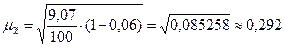
t (0,954; 100) = 2, следовательно предельная ошибка равна:
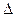 = 0,292 * 2 = 0,584 %.
= 0,292 * 2 = 0,584 %.
Тогда интервал для средней равен:
(11,1-0,584; 11,1+0,584) (10,516; 11,684)
Т.е. средняя влажность по всей партии товара с вероятностью 0,954 будет в интервале от 10,516 до 11,684%.
 2015-04-08
2015-04-08 2956
2956

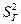 -
-