Средняя квадратическая (стандартная) ошибка выборки зависит от объема выборки и степени вариации признака в генеральной совокупности. Уменьшение стандартной ошибки выборки, а следовательно, увелечение точности оценки, всегда связано с увелечением объема выборки. Поэтому на стадии организации выборочного наблюдения необходимо определиться с объемом выборочной совокупности.
Из формул предельной ошибки выборочной средней для случая простой случайной повторной выборки:
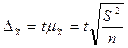 можно получить, что
можно получить, что 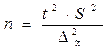
При проектировании выборочного наблюдения предполагается заранее заданной величина допустимой ошибки выборки в соответствии с задачами конкретного исследования (следует помнить, что в формуле для определения 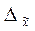 – есть абсолютная величина предельной ошибки выборки) и вероятность выводов по результатам наблюдения (величина коеффициента t соответствует принятому уровню доверительнойц вероятности).
– есть абсолютная величина предельной ошибки выборки) и вероятность выводов по результатам наблюдения (величина коеффициента t соответствует принятому уровню доверительнойц вероятности).
Величина s2 , характеризующая дисперсию признака в генеральной совокупности чаще всего бывает неизвестна. Для ее оценки используют приближенные способы:
· проводят «пробное» обследование (обычно небольшого объема), на базе которого определяется величина дисперсии, которая используется в качестве оценки генеральной дисперсии:
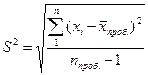 , где
, где 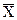 проб. – средняя арифметичсеская по результатам пробного обследования.
проб. – средняя арифметичсеская по результатам пробного обследования.
По данным нескольких пробных обследований выбирается наибольшее значение дисперсии
· Можно использовать данные прошлых выборочных обследований, проводившихся в аналогичных целях.
· Если распределения признака в генеральной совокупности может быть отнесено к нормальному закону распределения, то разность вариаций примерно равен 65 (крайние значения отстают в ту и другую сторону от средней на расстоянии 35), т.о. R=65 откуда S=1\6 R, где R=xmax-xmin – размах вариации.
Пример. Сколько продавцов в городе следует обследовать, чтобы получить характеристики среднего уровня оплаты труда продавцов?
Предположим, что разница между наивысшим и наименьшим уровнем оплаты труда продавцов в городе составляет 600 ден. ед.. Для нормального распределения в промежутках 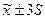 99.7% всех значений признака. Это означает, что s=600/6 или s=100 ден. ед. Для дальнейших расчетов достаточно, чтобы с вероятностью 0.954 предельная ошибка выборки не превышала 10 ден. ед. Тогда, зная s=100 ден. ед., а t=2 объем выборки будет:
99.7% всех значений признака. Это означает, что s=600/6 или s=100 ден. ед. Для дальнейших расчетов достаточно, чтобы с вероятностью 0.954 предельная ошибка выборки не превышала 10 ден. ед. Тогда, зная s=100 ден. ед., а t=2 объем выборки будет:
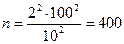 человек
человек
Таким образом, при заданных условиях следует обследовать размер заработной платы у 400 продавцов города.
В тех случаях когда задана не величина абсолютной предельной ошибки 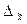 , а величина относительной погрешности, выраженная в процентах к средней:
, а величина относительной погрешности, выраженная в процентах к средней:
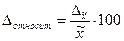 %
%
откуда
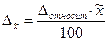
и формула для нахождения объема выборки примет вид:
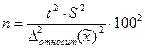 , но известно, что
, но известно, что 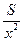 100%=V есть коэффициент вариации, откуда
100%=V есть коэффициент вариации, откуда 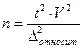
Пример: По данным пробного обследования коэффициент вариации составляет 25%. Сколько следует отобрать единиц в выборку, чтобы с вероятностью 0.954 предельная относительная ошибка выборки не превышала 5%?
При V=25%, 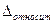 =5%, и t=2
=5%, и t=2
Имеем: 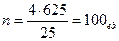
При определении по материалам выборки доли признака, а не средней его величины, объем выборочной совокупности определяется по следующим формулам:
· Для повторного объема
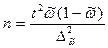
· Для бесповторного отбора
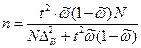
Для случая, когда частоты 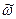 даже приблизительно неизвестны, можно произвести примерный расчет численности выборки, вводя в расчет максимальную величину дисперсии доли, равную 0.25, т.е.
даже приблизительно неизвестны, можно произвести примерный расчет численности выборки, вводя в расчет максимальную величину дисперсии доли, равную 0.25, т.е. 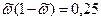 :
:
· Для повторного отбора
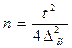 ,
,
· Для бесповторного отбора
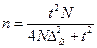
 2015-04-08
2015-04-08 863
863








