Проверка значимости полученного значения линейного коэффициента корреляции rxy ничего не говорит о том, насколько это значение может отличаться от точного значения. Ответ на этот вопрос дает построение доверительного интервала.
Под доверительным интервалом понимаются пределы, в которых лежит точное значение определяемого показателя с заданной вероятностью (P = 1-α).
Вычисленное на основании данных таблицы 1.1 значение rxy рассматривается как приближенное, отличающееся от точного значения линейного коэффициента корреляции, обозначаемого 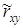 . Ставится задача определить такой интервал (r– , r+), который будет содержать точное значение
. Ставится задача определить такой интервал (r– , r+), который будет содержать точное значение 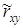 с заданной вероятностью.
с заданной вероятностью.
Если в границы доверительного интервала попадет нулевое значение, т. е. нижняя граница отрицательна, а верхняя положительна, то значение rxy принимается равным нулю, так как он не может одновременно принимать и положительное, и отрицательное значения.
Для статистически значимого коэффициента корреляции 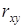 доверительный интервал получают с использованием Z- преобразования Фишера
доверительный интервал получают с использованием Z- преобразования Фишера 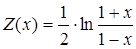 . Первоначально определяется приближенное значение величины z по формуле
. Первоначально определяется приближенное значение величины z по формуле
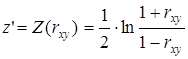 . (1.6)
. (1.6)
Затем для точного значения 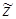 определяется интервальная оценка, т. е. вычисляются границы доверительного интервала (z– , z+), такого, что с заданной вероятностью выполняется условие z– <
определяется интервальная оценка, т. е. вычисляются границы доверительного интервала (z– , z+), такого, что с заданной вероятностью выполняется условие z– < 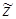 < z+
< z+
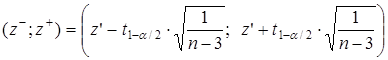 (1.7)
(1.7)
где t 1-α/2 – квантиль стандартного нормального распределения порядка 1–α/2.
Граничные значения доверительного интервала (r– , r+) для 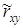 получаются из граничных значений доверительного интервала (z– , z+) для
получаются из граничных значений доверительного интервала (z– , z+) для 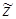 с помощью обратного Z- преобразования Фишера
с помощью обратного Z- преобразования Фишера 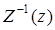
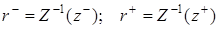 . (1.8)
. (1.8)
Контрольные вопросы:
1. Как вычисляется линейный коэффициент парной корреляции 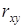 ?
?
2. Как осуществляется оценка статистической значимости линейного коэффициента парной корреляции 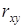 ?
?
3. Что называется уровнем значимости?
4. Как строится доверительный интервал для линейного коэффициента парной корреляции?
Задачи.
1. По величине коэффициента линейной корреляции r xy = 0,46 определить степень тесноты зависимости между признаками x и y. (Слабая).
2. Можно ли говорить о наличии линейной зависимости между переменными x и y, если по 52 наблюдениям было получено значение 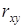 = 0,42. Ответ дать с вероятностью ошибки 5 %. (Можно).
= 0,42. Ответ дать с вероятностью ошибки 5 %. (Можно).
Лабораторная работа№ 1
Задание. На основании данных таблицы П1.1 для соответствующего варианта (табл. 1.3):
1. Вычислить линейный коэффициент парной корреляции 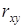 .
.
2. Проверить значимость коэффициента парной корреляции 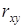 при заданном уровне значимости α.
при заданном уровне значимости α.
3. Построить доверительный интервал для значимого линейного коэффициента парной корреляции 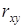 .
.
Таблица 1. 3
Варианты кривых выравнивания к лабораторной работе № 1
| Вариант | Графы из табл. П1.1 | Уровень значимости |
| 1, 2 | 0,05 | |
| 1, 3 | 0,025 | |
| 1, 4 | 0,01 | |
| 1, 5 | 0,05 | |
| 1, 6 | 0,025 | |
| 1, 7 | 0,01 | |
| 1, 8 | 0,05 | |
| 2,3 | 0,025 | |
| 2, 4 | 0,01 | |
| 2, 5 | 0,05 | |
| 2, 6 | 0,025 | |
| 2, 7 | 0,01 | |
| 2, 8 | 0,05 | |
| 3,4 | 0,025 | |
| 3,5 | 0,01 | |
| 3, 6 | 0,05 | |
| 3, 7 | 0,025 | |
| 3, 8 | 0,01 | |
| 4,5 | 0,05 | |
| 4,6 | 0,025 | |
| 4,7 | 0,01 | |
| 4,8 | 0,05 | |
| 5,6 | 0,025 | |
| 5,7 | 0,01 | |
| 5,8 | 0,05 |
Пример выполнения лабораторной работы№ 1
Исходные данные:
- наблюдаемые значения переменных x и y заданы в таблице 1.4;
- уровень значимости α = 0,05.
Таблица 1. 4
Исходные данные
| Области | x | y | Области | x | y | ||
| Белгородская | Рязанская область | ||||||
| Брянская | Смоленская | ||||||
| Владимирская | Тамбовская | ||||||
| Воронежская | Тверская | ||||||
| Ивановская | Тульская | ||||||
| Калужская | Ярославская | ||||||
| Костромская | Архангельская | ||||||
| Курская | Вологодская | ||||||
| Липецкая | Калининградская | ||||||
| Московская | Ленинградская | ||||||
| Орловская | Мурманская |
1) Вычисление σx, σy и 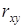 (1.3), (1.4). Используя данные таблицы 1.5 получим
(1.3), (1.4). Используя данные таблицы 1.5 получим
Таблица 1. 5
Промежуточные результаты расчетов
| Номер наблюдения | x | y | x 2 | y 2 | xy | 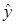 | (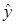 –y)2 –y)2 | (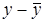 )2 )2 |
| 33,16 | 34,13 | 1,00 | ||||||
| 37,24 | 0,06 | 9,00 | ||||||
| 37,24 | 1,54 | 16,00 | ||||||
| 36,49 | 0,24 | 16,00 | ||||||
| 38,75 | 162,52 | 196,00 | ||||||
| 43,34 | 0,12 | 9,00 | ||||||
| 34,63 | 13,19 | 81,00 | ||||||
| 33,16 | 46,81 | 0,00 | ||||||
| 36,49 | 132,44 | 64,00 | ||||||
| 42,95 | 442,90 | 576,00 | ||||||
| 37,99 | 1,01 | 1,00 | ||||||
| 35,75 | 3,05 | 36,00 | ||||||
| 37,62 | 1,91 | 1,00 | ||||||
| 35,00 | 3,99 | 9,00 | ||||||
| 36,49 | 2,22 | 25,00 |
Продолжение таблицы 1. 5
| Номер наблюдения | x | y | x 2 | y 2 | xy | 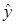 | (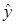 –y)2 –y)2 | (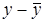 )2 )2 |
| 40,65 | 178,23 | 196,00 | ||||||
| 41,80 | 33,63 | 16,00 | ||||||
| 41,80 | 46,23 | 25,00 | ||||||
| 42,57 | 73,42 | 36,00 | ||||||
| 37,24 | 115,76 | 64,00 | ||||||
| 36,87 | 47,14 | 100,00 | ||||||
| 46,85 | 147,58 | 361,00 | ||||||
| Сумма | 844,081 | 1488,136 | ||||||
| Среднее значение | 126,91 | 16190,55 | 1683,545 | 5116,636 | 38,367 | 67,643 | 83,545 |
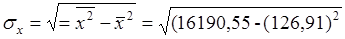 = 9,199,
= 9,199,
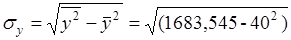 = 9,140,
= 9,140,
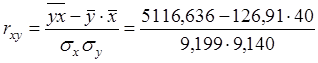 = 0,479.
= 0,479.
2) Проверка значимости 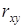 (1.5).
(1.5).
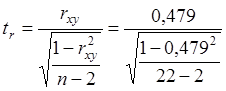 = 2,44.
= 2,44.
Для определения t крит может использоваться статистическая функция СТЬЮДРАСПОБР(0,05;20) из MS Excel, либо функция TINV(0,05;20) из OpenOffice.org Calc, либо таблица П4.2 из приложения.
При α = 0,05 и степени свободы k = n –2 = 20–2 = 20
t крит = t 1-α,n-2 = СТЬЮДРАСПОБР(0,05;20) =2,086.
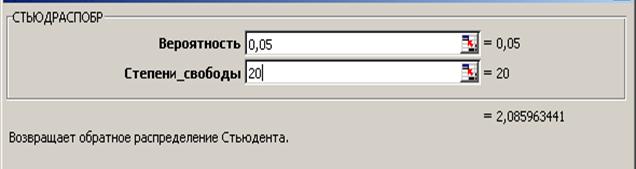
Рис. 1.1 Окно ввода параметров функции СТЬЮДРАСПОБР() MS Excel
Так как
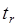 = 2,44 > t 1-α,n-2 = 2,086,
= 2,44 > t 1-α,n-2 = 2,086,
то делаем вывод о статистической значимости линейного коэффициента парной корреляции 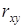 .
.
3) Построение доверительного интервала для линейного коэффициента корреляции 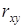 (1.8) – (1.10).
(1.8) – (1.10).
Определим величину z (1.8) Z- преобразования Фишера
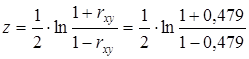 = 0,522.
= 0,522.
Для определения t 1-α/2 – квантиля стандартного нормального распределения порядка 1–α/2 = 1 – 0,05/2 = 0,975 может использоваться статистическая функция НОРМСТОБР(0,975) из MS Excel, либо функция NORMSINV(0,975) из OpenOffice.org Calc, либо таблицы П4.1 из приложения.
t 1-α/2 = НОРМСТОБР(0,975) = 1,96.
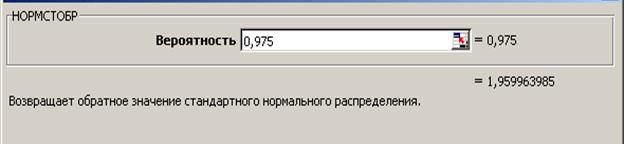
Рис. 1.3 Окно ввода параметров функции НОРМСТОБР() MS Excel
Для получения t 1-α/2 из таблицы П4.1 нужно использовать соотношение
1-α/2 – 0,5 = Ф(t 1-α/2),
т. е. нужно определить ячейку (клетку) таблицы П4.1, содержащую значение 1-α/2 – 0,5 и сложить значение t, соответствующее данной строке с номером столбца, умноженным на 0,01: t 1-α/2 = t + Nстолбца·0,01.
Так как α = 0,5, 1-α/2 – 0,5 = 1 – 0,05/2 -0,5 = 0,475. Ячейке, содержащей число 0,475, соответствуют t = 1,9 и Nстолбца = 6, поэтому
t 1-α/2 = t + Nстолбца·0,01 = 1,9 + 0,06 = 1,96.
Вычислим 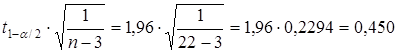 .
.
Вычислим границы доверительного интервала (z– , z+) для величины z
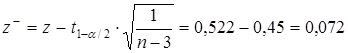 ,
,
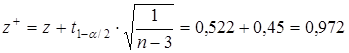 .
.
Определим граничные значения доверительного интервала (r– , r+), содержащего коэффициент корреляции rxy.
Для определения значения 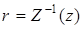 может использоваться статистическая функция ФИШЕРОБР(z)) из MS Excel, либо функция FISHERINV(z) из OpenOffice.org Calc.
может использоваться статистическая функция ФИШЕРОБР(z)) из MS Excel, либо функция FISHERINV(z) из OpenOffice.org Calc.
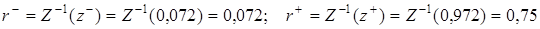 .
.
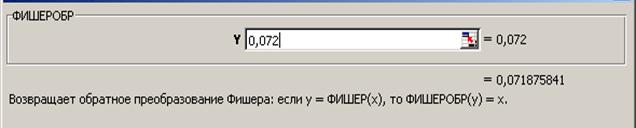
Рис. 1.4 Окно ввода параметров функции ФИШЕРОБР() MS Excel
Искомый доверительный интервал для rxy имеет вид (0,072; 0,75).
Результаты:
1) 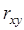 = 0,479.
= 0,479.
2) Коэффициент rxy статистически значим.
3) Доверительный интервал для rxy – (0,072; 0,75).
 2015-04-08
2015-04-08 5641
5641
