Точечные статистические оценки не несут информации о точности полученных результатов, т.к. в результате мы имеем только одно значение.
Найдем интервал 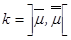 . Таким образом, чтобы для заданной вероятности
. Таким образом, чтобы для заданной вероятности 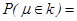 g.
g.
Где m - теоретическое значение оцениваемой числовой характеристики, g -доверительная вероятность или надежность.
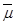 и
и 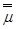 - нижние и верхние границы интервала, они являются статистиками подлежащими определению. Тогда разница
- нижние и верхние границы интервала, они являются статистиками подлежащими определению. Тогда разница 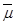 -
- 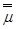 - длина доверительного интервала и длина доверительного интервала зависит от объема выборки и доверительной вероятности, причем она увеличивается при уменьшении объема выборки и увеличении доверительной вероятности. При g =1 доверительный интервал совпадает со множеством значений оцениваемой числовой характеристики m.
- длина доверительного интервала и длина доверительного интервала зависит от объема выборки и доверительной вероятности, причем она увеличивается при уменьшении объема выборки и увеличении доверительной вероятности. При g =1 доверительный интервал совпадает со множеством значений оцениваемой числовой характеристики m.
1 Оценка математического ожидания нормальной случайной величины в случае известной дисперсии.
Пусть x принадлежит нормальному закону распределения
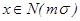
причем дисперсия s2 известна, необходимо по выборке
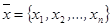
построить доверительный интервал для математического ожидания m:
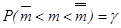
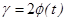 , где
, где 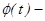 функция Лапласа, t- находится по таблице.
функция Лапласа, t- находится по таблице.
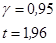
При этом необходимо, чтобы длина доверительного интервала была минимальной при заданной вероятности. Из теории вероятности известно, что при сделанных предположениях, статистика
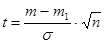
m1 -выборочная средняя или 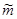 распределена по нормальному закону, что N(0;1), где функция четная.
распределена по нормальному закону, что N(0;1), где функция четная.
Выбирая для t - доверительный интервал симметричный относительно начала координат, при этом длина интервала будет минимальной, получим, что 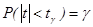 , т.е. случайное событие
, т.е. случайное событие 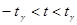 эквивалентно неравенству
эквивалентно неравенству
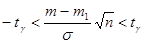 .
.
Умножим, выразим, получим доверительный интервал
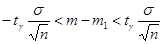 ,
,
m 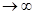 - высокая точность интервальной оценки, на практике t не берут близким к 1, в этом случае точность оценки будет высока.
- высокая точность интервальной оценки, на практике t не берут близким к 1, в этом случае точность оценки будет высока.
2 Оценка математического ожидания нормальной случайной величины в случае неизвестной дисперсии.
В отличие от рассмотренного случая статистика t рассматривается как
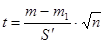 .
.
где m1 - также выборочная средняя;
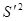 - исправленная выборочная дисперсия;
- исправленная выборочная дисперсия;
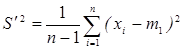
Из теории вероятности известно, что статистика t имеет распределение Cтъюдента, говорят с (n- 1 ) степенью свободы.
Аналогично предыдущему случаю:
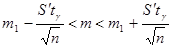 ;
;
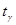 - ищется по таблице распределения Стъюдента с (n- 1 ) степенью свободы.
- ищется по таблице распределения Стъюдента с (n- 1 ) степенью свободы.
Если число степеней свободы >30, то распределение Стъюдента практически совпадает со стандартным нормальным законом.
3 Оценка дисперсий нормальной случайной величины в случае известного математического ожидания.
В этом случае статистика 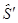 -состоятельная несмещенная оценка дисперсий.
-состоятельная несмещенная оценка дисперсий.
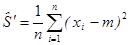
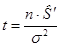 .
.
Если раскрыть это соотношение, то
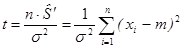
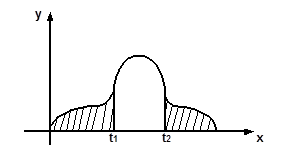 |
Эта статистика имеет распределение Пирсона с -степенями свободы, график этого распределения выглядит следующим образом
t1 и t2 выбирают так, чтобы 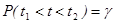
т.е. заштрихованная на рисунке площадь под графиком равна доверительной вероятности.
Условие минимума длины доверительного интервала
f(t1)= f(t2).
На практике удовлетворить этому условию трудно, поэтому поступают так:
Берут t1 и t2 и такими, чтобы заштрихованные на рисунке площади совпадали, тогда вероятность того, что
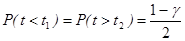 ;
;
Тогда доверительный интервал для дисперсии
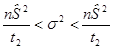 .
.
При большом числе степеней свободы >30, распределение Пирсона совпадает с нормальным распределением.
4. Оценка дисперсии нормальной случайной величины в случае неизвестного математического ожидания.
Статистика t будет определяться таким образом, как
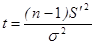
и распределение осуществляется по закону
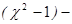 степень свободы распределения Пирсона.
степень свободы распределения Пирсона.
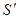 -исправленная выборочная оценка.
-исправленная выборочная оценка.
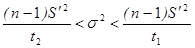 ;
;
Причем t1 и t2 находим из таблиц 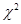 распределения Пирсона с (n- 1 ) степенью свободы по заданной доверительной вероятности
распределения Пирсона с (n- 1 ) степенью свободы по заданной доверительной вероятности 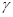 .
.
 2015-10-16
2015-10-16 1271
1271








