Колориметрические системы. Основы их построения

Первая стандартная колориметрическая система была принята в 1931 году на VIII сессии Международной комиссии по освещению — МКО (С1Е). Резолюцией МКО в качестве трех линейно независимых цветов были выбраны следующие монохроматические излучения: красный К (к ^ш 700 нм, легко выделяемый красным светофильтром из спектра лам­пы накаливания); зеленый С (X = 546,1 нм — линия е в спектре ртутной лампы); синий В (X = 435,8 нм — линия § в спектре ртутной лампы).

Восприятие цвета на упаковке 149

Колориметрическая система, использующая эти цвета в качестве основных, получила название С1ЕКСВ (КСВ происходит из сокраще­ний соответствующих английских слов: К — гее! — красный; С — §гееп — зеленый; В — Ыие — синий).

Сразу же следует особо отметить, что в современной литературе, в которой описывается обработка цветных изображений с помощью ком­пьютеров, встречается также термин «система КСВ». Однако в отли­чие от системы МКО речь в данном случае идет о цветах КСВ, имею­щих специфическую принадлежность к характеристикам цветопреоб-разующих узлов сканера или видеомонитора. У этих цветов нет фикси­рованных длин волн, относительно которых проводятся все измерения, и поэтому термин «система КСВ» здесь вряд ли уместен.

На сессии МКО в том же 1931 году была принята еще одна крас-кикраскикраскикраскикраскикраскикраскикраскиколориметричес-кая система. Ее составляющие цвета были более насыщенными, чем спектральные. Поскольку таких цветов в природе нет, то она получила название С1ЕХУ2. Данная колориметрическая система была получена искусственно, путем пересчета из цветовых координат С1ЕКСВ. Вы­бор цветов ХУ2 вытекал из задач, поставленных при разработке этой системы, основные из которых: упрощение расчетов и отсутствие отри­цательных координат, что неизбежно, если за основные принимать цве­та С1ЕКСВ.

В настоящее время рабочей является международная колориметри­ческая система С1ЕХУ2. В ней обычно выражают результаты измере­ний, а система С1ЕКСВ выполняет вспомогательную, иногда конт­рольную функцию. Тем не менее следует еще раз отметить, что именно система С1ЕКСВ явилась основой системы С1ЕХУ2.

5.7.2. Общие сведения о цветовом пространстве

Из рассмотренных ранее законов Грассмана следует, что цвет мож­но выразить точкой в трехмерном пространстве. Трехмерное простран­ство для геометрического изображения цвета принято называть цвето­вым пространством. В нем каждому цвету будет соответствовать опре­деленная точка, а каждой точке пространства — соответствующий цвет.

В цветовой координатной системе каждый цвет выражается через основные цвета этой системы. Причем, как было отмечено ранее, они должны быть линейно независимы (то есть ни один из них не должен получаться сложением двух других). Положение точки в пространстве, характеризующей тот или иной цвет, задается тремя координатами. Эту

150 Глава 5

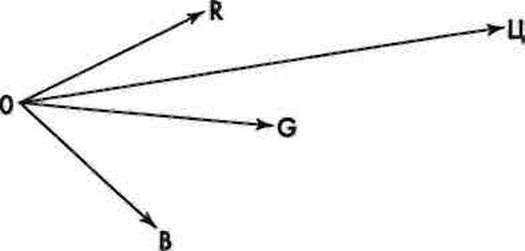Рис. 5.29. Вектор цвета в произвольной системе координат

же точку можно рассматривать и как конец вектора, проведенного из начала координат в выбранной системе, например КСВ (рис. 5.29).

Положение самого цветового вектора в цветовом пространстве и его длина не зависят от выбора основных цветов, а определяются цветнос­тью и яркостью цвета. Вектор цвета любого излучения можно предста­вить цветовым уравнением.

Для начала рассмотрим, что из себя представляет цветовое простран­ство на примере произвольных цветов КСВ (в принципе можно выб­рать любую произвольную систему цветов, на рассмотрение сути дела это никак не повлияет).

Выразим некоторый цвет Ц в виде цветового уравнения. Цветовым уравнением называется уравнение, показывающее, в каких количествах нужно взять основные цвета, чтобы в результате их смешения получить цвет, зрительно неотличимый от выражаемого уравнением. Пусть в на­шем случае Ц — выражаемый уравнением цвет; К, С, В — цветовые ко­ординаты цвета Ц в системе основных КСВ или, иными словами, коли­чества основных, необходимые для получения цвета Ц; К, С, В — цвета излучений, принятые за основные. Тогда, в нашем случае, цветовое урав­нение можно записать следующим образом:

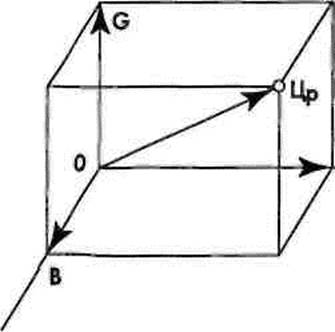
Ц=КК + СС + ВВ. Сравнив это уравнение с уравнени­ем свободного вектора в пространстве, рассматриваемым в векторной алгебре, а ^т хг + у] + г%, где %],% — тройка еди­ничных векторов, легко убедиться, что они практически идентичны.

В нашем случае координаты цвета

Рис. 530. Вектор цвета в ^{КСВ б}У^ определять проекции век-

прямоугольной системе тора цвета на координатные оси цве-

координат тового пространства. Направление

координатных осей можно выбирать

Восприятие цвета на упаковке

любое, но удобней принять цветовую координатную систему прямоу­гольной (рис. 5.30).

На первый взгляд, рассматривать цвет в виде вектора в простран­стве представляется бессмысленным. И в самом деле, вопрос о том, куда направлен вектор, например, желтого цвета, выглядит довольно стран­ным. Тем не менее в рассматриваемом цветовом пространстве КСВ этот вектор имеет вполне определенное направление. Если он находится в плоскости СК и лежит ближе к оси С, то имеет зеленый оттенок, а если лежит ближе к оси К, то имеет красноватый оттенок. Таким образом, мож­но сказать, что направление вектора зависит от соотношения цветовых координат и характеризует цветность. Длина же самого вектора цвета зависит от суммы цветовых координат и выражает яркость. Вектор Ц соответствует цветам одинаковой цветности, но различной яркости.

В цветовом пространстве в виде вектора можно представить и ахромати­ческие цвета. Это возможно, когда координаты цвета (в нашем случае КСВ) равны между собой. В этом случае яркость цвета увеличивается по вектору от начала координат к концу, то есть от черного цвета через серый к белому. Этот вектор называется ахроматической осью. Соответственно чем больше значения цветовых координат, тем больше яркость цвета. По мере удаления от ахроматической оси увеличивается насыщенность цвета

В современной терминологии часто используются такие понятия, как треугольник цветности, диаграмма цвет­ности, локус, цветовой охват. Что это та­кое, как они образуются и для чего нуж­ны, будет рассмотрено далее.

А начнем рассмотрение этих понятий с принципа образования плоскости единич­ных цветов на примере системы С1ЕК.СВ.

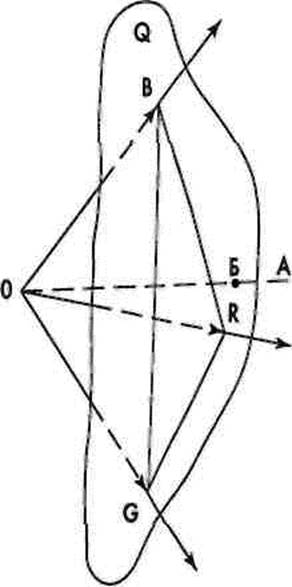
Плоскость единичных цветов () (рис. 5.31), проходит через отложенные на осях координат яркости единичных значений выбранных основных цветов. Единичным цветом в колориметрии на­зывают цвет, сумма координат которого (или по-другому модуль цвета т) равна 1. Поэтому можно считать, что плоскость О, пересекающая оси координат в точках В„ (К-1, С~0, В-0), В_с (К=0, С-1, В=0), В_в (Кг=0, С=0, В^в1), является единичным местом точек в пространстве С1ЕКСВ.

цветов и образование треугольника

Каждой точке плоскости единичных ^^с> ^^Плоск<>сть единичных

цветности

цветов (I соответствует след цветового

152 Глава 5

вектора, пронизывающего плоскость в соответствующей точке с тл=1. Следовательно, цветность любого излучения может быть представлена на плоскости единственной точкой. Можно себе представить и точку, соответствующую белому цвету (Б). Она образуется путем пересече­ния ахроматической оси (А) с плоскостью (2 (рис. 5.31).

Независимо от выбранной колориметрической системы плоскость единичных цветов, пересекаясь с координатными осями, образует треу­гольник, называемый цветовым треугольником или треугольником цвет-посты (см. рис. 5.31). В вершинах треугольника находятся точки основ­ных цветов. Определение точек цветов, получаемых смешением любых трех основных, производится по правилу графического сложения.

В колориметрии для описания цветности нет необходимости прибе­гать к пространственным представлениям. Достаточно использовать плоскость треугольника цветности. В нем положение точки любого цвета может быть задано только двумя координатами. Третью легко найти по двум другим, так как сумма координат цветности (или модуль) всегда равна 1. Поэтому любая пара координат цветности может служить ко­ординатами точки в прямоугольной системе координат на плоскости. В дальнейшем для рассуждений будет использована именно эта прямоу­гольная система.

Итак, мы выяснили, что цвет графически можно выразить в виде вектора в пространстве или в виде точки, лежащей внутри треугольни­ка цветности.

5.7.2.1. Диаграмма цветности г§

Определим с помощью треугольника цветности границы реально наблюдаемых цветов. Поскольку цветов более насыщенных, чем спект­ральные, не существует, то точки цветов, их выражающие, и будут оп­ределять эту границу.

Нанесем на цветовой треугольник значения координат цветности, соответствующие спектральным излучениям от 380 до 700 нм. Для это­го воспользуемся кривыми сложения 7(Х),§(Х)_}Ь (Я), представляющи­ми собой функции распределения по спектру цветовых координат мо­нохроматических излучений мощностью в 1 Вт (рис. 5.32). Такие коор­динаты называются удельными. С их помощью определим положение точек, соответствующих координатам цветности монохроматических излучений (рис. 5.33). Соединив эти точки, получим линию спектраль­ных цветов. Кривая получается разомкнутой. Ее граничные точки соот­ветствуют максимально насыщенным красному (к =700 нм) и фиоле­товому (X =380 нм) цветам. Замкнув концы граничных точек прямой

Восприятие цвета на упаковке

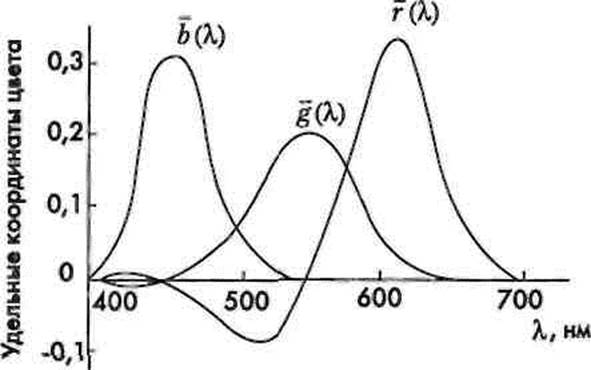Рис.532. Кривые сложения г(Х),§(Х),Ь(к)

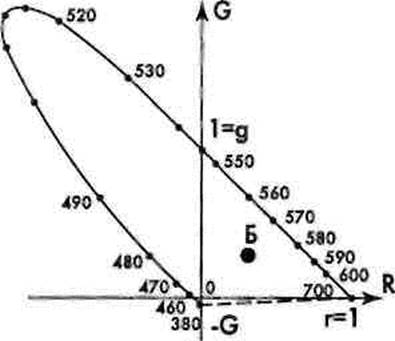(на графике пунктирная линия), по­лучим геометрическое место точек максимально насыщенных пурпур­ных цветов. Поскольку пурпурных доо цветов в спектре нет (пурпурные цве- Х.нм та представляют собой смесь красных и фиолетовых излучений), то и на пунктирной линии отсутствуют зна­чения длин волн. Линия, являющая- _ц

Рис. 5.33. Локус в цветовом треугольнике

ся геометрическим местом точек цветности монохроматических излу­чений и замкнутая линией пурпур­ных, называется локусом (лат. 1осиз — место) (см. рис. 5.33). Внутри локуса

находятся все реальные цвета. Вне локуса лежат воображаемые (или, как их еще часто называют, нереальные) цвета, более насыщенные, чем спектральные, выраженные в данной колориметрической системе.

Общими свойствами любого локуса, независимо от типа выбранной колориметрической системы, являются:

1) точка белого цвета имеет координаты (0,33; 0,33);

2) насыщенность цветов возрастает от белой точки к локусу;

3) на прямой, соединяющей белую точку с локусом, лежат цвета оди­накового цветового тона, но разной насыщенности.

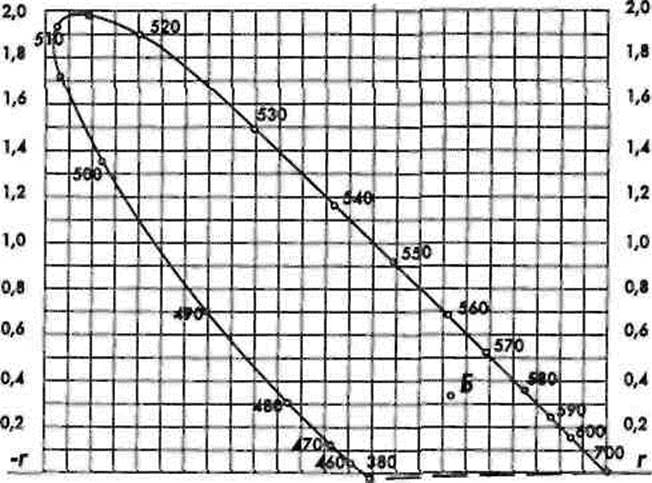
Нанеся на локус сетку прямоугольных координат, получают диаг­рамму цветности (рис. 5.34). С ее помощью можно определять качествен­ные характеристики цвета — доминирующую длину волны (характери-

Глава 5

-1,4 -1,2 -1,0 -0,8 -0,6 -0,4 -0,2

-1,4 -1,2 -1,0 -0,8 -0,6 -0,4 -0,2

9

0,2 0,4 0,6 0,8 1,0

0,2 0,4 0,6 0,8 1,0

Рис. 5.34. Диаграмма цветности щ

зует цветовой тон) и чистоту цвета (характеризует насыщенность) того или иного цвета. Площадь, ограниченная локусом и замыкающей его линией пурпурных цветов, называется полем реальных цветов.

Как видно из рис.5.34, цветности большинства излучений характе­ризуются отрицательной координатой г < 0, а у пурпурных § < 0. Это затрудняет расчеты цвета по его спектральному составу. Кроме того, определение яркости цветов в системе С1ЕКСВ связано с расчетом всех трех координат цвета.

5.7.2.2. Диаграмма цветности ху

Одним из основных условий, положенных в основу стандартной колориметрической системы ХУ2, было то, что координаты цветности всех реальных цветов системы С1ЕКСВ должны лежать внутри треугольника цветности хуг. Точка белого цвета на диаграмме ху должна иметь коорди­наты 0,33; 0,33 (так же, как и на диаграмме г§), что соответствует равно-энергетическому источнику Е. В процессе пересчета из колориметричес­кой системы КСВ в С1ЕХУ2 это удалось сделать. Были преобразованы и

кривые сложения г(Х),§(Х)_уЬ(Х) в ^(А.),у(Я),1(Л) (рис. 5.35). Распре­деление удельной координаты у "/(Я) соответствует координатам отно­сительной спектральной чувствительности глаза V =/(Я), что позволяет определять яркость одной этой координатой. Цвета X и 2 не имеют ярко­сти.

Восприятие цвета на упаковке

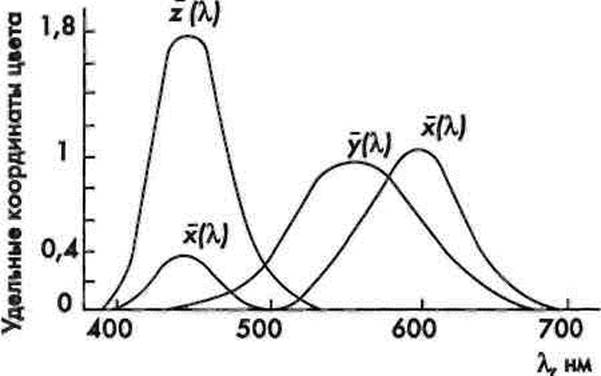
Рис. 5.35. Кривые сложения #(Я),г/(Л),2(Л]

На рис.5.36 представлен локус в цветовом треугольнике хуг. Как видно из рисунка, отрицательные координаты здесь отсутствуют. На­неся сетку координат на локус, получим диаграмму цветности осу (рис.5. 37, вкладка).

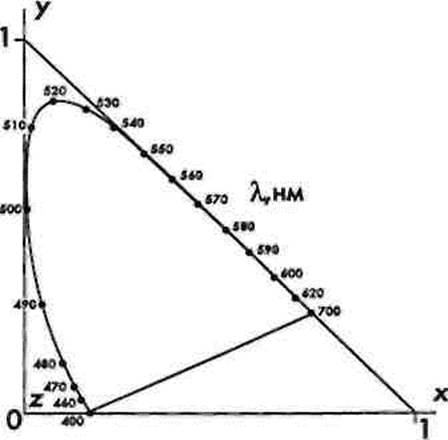
Рис. 53В. Локус в цветовом треугольнике луг

При определении по диаграмме ху психофизических цветовых ха­рактеристик — доминирующей длины волны и чистоты цвета — учиты­вают тип стандартного источника МКО, относительно которого и оп­ределяют эти параметры.