Пусть X – наблюдаемая дискретная или непрерывная случайная величина. Статистической гипотезой 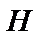 называется утверждение, в котором высказывается предположение относительно параметров или вида закона распределения случайной величины X. Гипотеза H называется простой, если она содержит только одно предположение, а гипотеза, которая состоит из конечного или бесконечного числа простых гипотез, называется сложной. Гипотезы о значениях параметров известного распределения случайной величины
называется утверждение, в котором высказывается предположение относительно параметров или вида закона распределения случайной величины X. Гипотеза H называется простой, если она содержит только одно предположение, а гипотеза, которая состоит из конечного или бесконечного числа простых гипотез, называется сложной. Гипотезы о значениях параметров известного распределения случайной величины 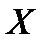 называются параметрическими. Непараметрическими называются гипотезы, сформулированные относительно вида закона распределения случайной величины X. Основная выдвинутая гипотеза называется нулевой H 0.
называются параметрическими. Непараметрическими называются гипотезы, сформулированные относительно вида закона распределения случайной величины X. Основная выдвинутая гипотеза называется нулевой H 0.
Гипотеза, противоречащая нулевой гипотезе H 0, называется альтернативной (конкурирующей) гипотезой 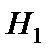 . Выбор альтернативной гипотезы определяется конкретной формулировкой задачи.
. Выбор альтернативной гипотезы определяется конкретной формулировкой задачи.
Правило, по которому принимается решение принять или отклонить гипотезу H 0, называется критерием K. Случайная величина 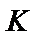 , с помощью которой принимается решение о принятии или отклонении нулевой гипотезы, называется с татистикой K критерия K. Проверка статистической гипотезы основывается на принципе отношения правдоподобия: маловероятные события считаются невозможными, а события, имеющие большую вероятность, считаются достоверными. Зафиксируем некоторую малую вероятность
, с помощью которой принимается решение о принятии или отклонении нулевой гипотезы, называется с татистикой K критерия K. Проверка статистической гипотезы основывается на принципе отношения правдоподобия: маловероятные события считаются невозможными, а события, имеющие большую вероятность, считаются достоверными. Зафиксируем некоторую малую вероятность 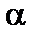 – уровень значимости. Пусть W – множество значений статистики K,
– уровень значимости. Пусть W – множество значений статистики K, 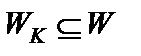 – такое подмножество, для которого
– такое подмножество, для которого 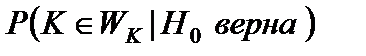 =
= 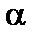 .
.
Наблюдаемым значением 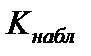 называется значение статистики
называется значение статистики 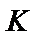 , вычисленное по выборке
, вычисленное по выборке 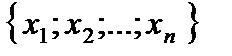 из генеральной совокупности случайной величины
из генеральной совокупности случайной величины 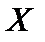 . Правило проверки статистических гипотез состоит в следующем:
. Правило проверки статистических гипотез состоит в следующем:
· если 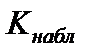
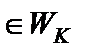 , то гипотеза
, то гипотеза 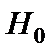 отклоняется с вероятностью
отклоняется с вероятностью 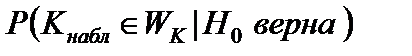 =
= 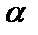 ,
,
· если 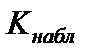
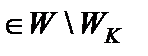 , то гипотеза H 0 принимается с вероятностью
, то гипотеза H 0 принимается с вероятностью 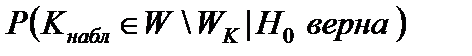 =1–
=1– 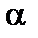 .
.
Критерий, основанный на использовании заранее заданного уровня значимости 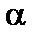 , называется критерием значимости. Вероятность р = 1 – a называется доверительной вероятностью.
, называется критерием значимости. Вероятность р = 1 – a называется доверительной вероятностью.
Критической областью WK называется совокупность значений статистики 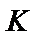 , при которых нулевую гипотезу отвергают. Областью принятия гипотезы называется совокупность значений W / WK статистики K, при которых нулевая гипотеза принимается. Критическими точками Kkp называются точки, отделяющие критическую область WK от области принятия гипотезы W / WK. Уровень значимости
, при которых нулевую гипотезу отвергают. Областью принятия гипотезы называется совокупность значений W / WK статистики K, при которых нулевая гипотеза принимается. Критическими точками Kkp называются точки, отделяющие критическую область WK от области принятия гипотезы W / WK. Уровень значимости 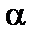 определяет «размер» критической области WK. Положение критической области на множестве статистики W зависит от вида нулевой и альтернативной гипотез. Возможны три вида расположения критической области:
определяет «размер» критической области WK. Положение критической области на множестве статистики W зависит от вида нулевой и альтернативной гипотез. Возможны три вида расположения критической области:
· правосторонняя критическая область 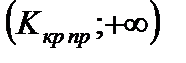 ;
;
· левосторонняя критическая область 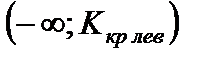 ;
;
· двусторонняя критическая область 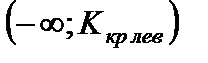

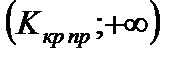 .
.
Точки Ккр пр, Ккр лев определяются в зависимости от вида закона распределения статистики К при выбранном уровне значимости a.
Выбор между гипотезами Н 0 и Н 1 может сопровождаться ошибками двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная нулевая гипотеза Н 0. Вероятность ошибки первого рода равна уровню значимостиa:
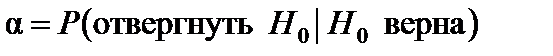 .
.
Ошибка второго рода состоит в том, что будет принята неправильная нулевая гипотеза Н 0 с вероятностью 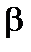 :
:
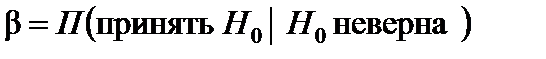 .
.
Вероятности ошибок должны быть малыми и выбираться заранее.
При проверке гипотезы возникает одна из следующих четырех ситуаций, приведенных в табл. 5.
Таблица 5. Ошибки первого и второго рода
| Результаты проверки гипотезы | Возможные состояния гипотезы | |
| H 0 верна | H 0 неверна | |
| Гипотеза H 0 отклоняется | Ошибка первого рода | Правильный вывод |
| Гипотеза H 0 принимается | Правильный вывод | Ошибка второго рода |
Мощностью критерия называется вероятность попадания статистики 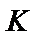 в критическую область
в критическую область 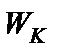 при условии, что справедлива конкурирующая (альтернативная) гипотеза
при условии, что справедлива конкурирующая (альтернативная) гипотеза 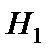 . Мощность критерия равна вероятности
. Мощность критерия равна вероятности 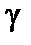 правильного отклонения нулевой гипотезы
правильного отклонения нулевой гипотезы 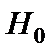 :
:
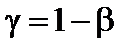 =
= 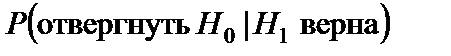 .
.
Поскольку критическая область 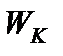 определяется по-разному на заданном уровне значимости
определяется по-разному на заданном уровне значимости 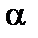 , то она выбирается так, чтобы мощность критерия
, то она выбирается так, чтобы мощность критерия 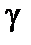 была возможно большей:
была возможно большей:
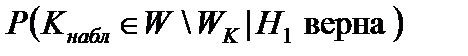 →
→ 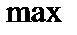 .
.
Чем больше мощность критерия, тем меньше вероятность принятия неверной гипотезы. Мощность критерия позволяет выбрать оптимальную статистику K для проверки гипотезы среди возможных статистик критерия.
На практике в качестве статистики K чаще всего используются специально подобранные случайные величины, распределения которых известны:
· Z (стандартизированное нормальное распределение);
· t (распределение Стьюдента);
· 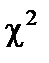 (закон Пирсона
(закон Пирсона 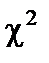 );
);
· F (распределение Фишера).
Высказываемые в ходе решения задач гипотезы условно подразделяются на следующие типы:
· о виде закона распределения исследуемой случайной величины;
· об однородности двух или нескольких выборок;
· о числовых значениях параметров исследуемого признака;
· об общем виде зависимости, существующей между компонентами исследуемого многомерного признака.
Общая схема проверки статистических гипотез. Несмотря на разнообразие гипотез и применяемых статистик, проверка статистических гипотез может быть проведена в виде следующей общей схемы:
1. На основании выборочных данных выдвигаются нулевая гипотеза 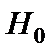 и альтернативная ей гипотеза
и альтернативная ей гипотеза 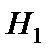 .
.
2. Выбирается уровень значимости a (в практических задачах пользуются стандартными значениями уровня значимости: 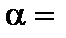 0,1; 0,05; 0,025; 0,01; 0,005; 0,001).
0,1; 0,05; 0,025; 0,01; 0,005; 0,001).
3. Выбирается статистика K, имеющая известный закон распределения.
4. Вычисляется наблюдаемое значение статистики Kнабл по выборочным данным.
5. Определяется вид критической области из условия 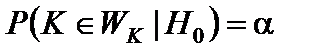 и область принятия гипнозы в зависимости от формулировки альтернативной гипотезы.
и область принятия гипнозы в зависимости от формулировки альтернативной гипотезы.
6. Принимается статистическое решение: если Kнабл попадает в критическую область, то нулевая гипотеза H 0 отвергается, в противном случае H 0 принимается.
Тест 8.1. Критическая область для проверки гипотезы H 0 имеет вид 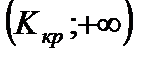 . Гипотеза будет отвергнута, если:
. Гипотеза будет отвергнута, если:
1) 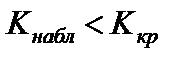 ;
;
2) 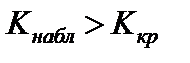 ;
;
3) 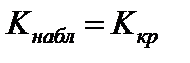 ;
;
4) 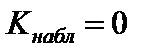 ;
;
5) 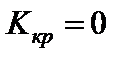 .
.
Тест 8.2. Критическая область для проверки гипотезы H 0 имеет вид: 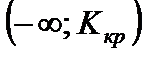 . Гипотеза будет отвергнута, если:
. Гипотеза будет отвергнута, если:
1) 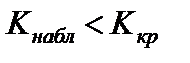 ;
;
2) 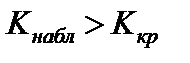 ;
;
3) 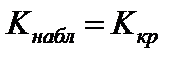 ;
;
4) 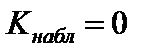 ;
;
5) 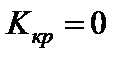
Тест 8.3. Область принятия гипотезы 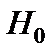 имеет вид
имеет вид 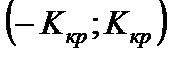 . Гипотеза
. Гипотеза 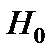 будет принята, если:
будет принята, если:
1) 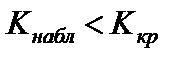 ;
;
2) 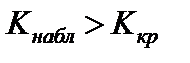 ;
;
3) 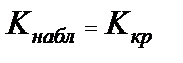 ;
;
4) 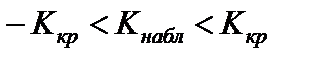 ;
;
5) 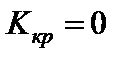
Изучение реальных процессов предполагает получение не только прогнозной оценки исследуемого показателя, но и количественной характеристики степени влияния на него различных факторов, а также оценки возможных последствий их изменений в будущем. В результате опыта проводятся наблюдения над целым рядом случайных величин. При этом возникает задача изучения взаимосвязи между случайными величинами, которая решается в три этапа:
· проводится оценка существенности влияния одного фактора на другой с помощью дисперсионного анализа;
· проводится численная оценка связи с помощью корреляционного анализа;
· строятся функциональные зависимости посредством регрессионного анализа.
Дисперсионный анализ служит для статистического установления влияния отдельных факторов на изменчивость какого-либо признака, значения которого могут быть получены опытным путем в виде выборки из генеральной совокупности случайной величины X. Под факторами понимаются различные независимые показатели, количество которых может быть различным. Конкретная реализация фактора А называется уровнем (группой) этого фактора. В зависимости от количества факторов различают однофакторный и многофакторный дисперсионный анализ. Величина X называется результативным признаком (фактором) Y. Идея дисперсионного анализа состоит в том, что дисперсия признака Y разлагается на сумму дисперсии, вызванной влиянием факторов, дисперсии, вызванной взаимодействием факторов и случайной дисперсии, вызванной неучтенными случайными факторами. Затем указанные дисперсии сравниваются и проверяются по статистическим критериям.
Однофакторный дисперсионный анализ позволяет статистически обосновать степень влияния на результативный признак Y одного фактора A.
Дисперсионный анализ рассматривает влияние двух независимых факторов A и B на изменчивость результативного признака Y.
Тест 8.4. Пусть в результате измерения величины M получено значение X, и пусть на процесс измерения влияют случайные независимые факторы A и B. Тогда для оценки значимости факторов A и B применяют:
1) однофакторный дисперсионный анализ;
2) двухфакторный дисперсионный анализ;
5) трехфакторный дисперсионный анализ.
Вопросы для самоконтроля
1. Что называется критерием и мощностью критерия?
2. Что определяет уровень значимости гипотезы?
3. Что такое критическая область критерия?
4. Как найти доверительную вероятность статистического критерия?
5. Какие виды ошибок могут быть при проверке гипотез?
6. Что называется мощностью критерия?
7. Какие статистики используются при проверке гипотез о законе распределения?
8. В чем заключается суть дисперсионного анализа?
9. В каком случае используется однофакторный дисперсионный анализ?
10. В чем разница между однофакторным и двухфакторным анализами?
 2015-04-20
2015-04-20 930
930








