Числовые характеристики выборки

Пусть случайный эксперимент описывается случайной величиной X, распределение которой зависит от одного или несколько параметров. К ним, в частности, относятся среднее, мода, медиана, среднее квадратичное отклонение, дисперсия, коэффициенты эксцесса и асимметрии, размах вариации, называемые параметрами генеральной совокупности. При исследовании случайной величины X из генеральной совокупности ее возможных значений извлекается выборка 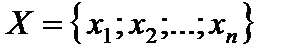объема n. По данной выборке можно приближенно вычислить значения каждого из изучаемых параметров, которые в статистике называются числовыми оценками параметров или просто оценками.

Данные характеристики условно разбиваются на четыре группы:

· показатели положения вариант на числовой оси;

· показатели разброса вариант относительно своего центра, определяющие кучность данных около центра;

· показатели асимметрии распределения вариант около своего центра;

· показатели, описывающие закон распределения.

Пусть выборка задана вариационным рядом (табл. 4).

Таблица 4. Вариационный ряд

Варианты X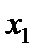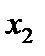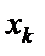
Относительные частоты wi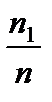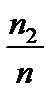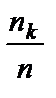

Выборочным средним значением выборки называется число, определяемое по формуле 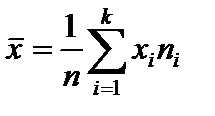, где x_i – варианта с частотой n_i, n – число наблюдений, 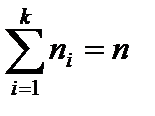. Если частоты 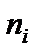равны единице, то k = n. При достаточно больших n используют формулу: 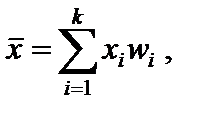где k – число значений вариационного ряда, w_i – относительная частота варианты x_i.

Выборочной медианой называется значение признака, находящегося в середине вариационного ряда. Если число вариант нечетно, т. е. 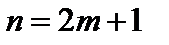, то медианой является (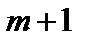)-я варианта (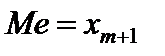); если же число вариант четно, то медиана равна среднему арифметическому двух значений в середине ряда: .

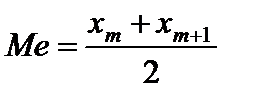Выборочной модой (Мо) называется варианта выборки, имеющая наибольшую частоту. Если несколько соседних значений имеют наибольшую частоту, то модой является их среднее арифметическое:

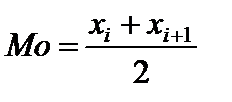, где для вариант 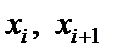частоты 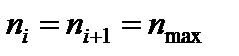. Если две или более несмежных вариант имеют разные наибольшие частоты, то ряд называется полимодальным. Если же все варианты встречаются одинаково часто, то ряд моды не имеет.

Мода и медиана используются в качестве характеристики среднего положения в случае, если границы ряда нечеткие или если ряд не симметричен.

Для описания рассеивания значений случайной величины относительно выборочного среднего используются выборочная дисперсия и выборочное среднее квадратическое отклонение.

Выборочной дисперсией значений выборки { x ₁, x ₂,…, x_n } называется число, определяемое по формуле

.

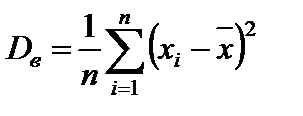После преобразований получается следующая формула:

.

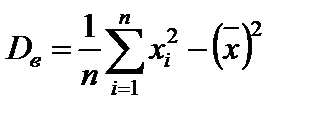Если задан вариационный ряд, то используется формула 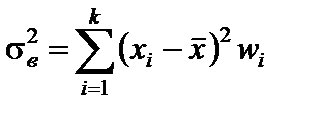, где k – число вариант, w_i – относительная частота варианты .

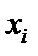Выборочным средним квадратическим отклонением называется число, которое находится по формуле .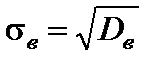

Пример 7.2. Выборка задана распределением частот

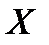	-1

Найти выборочную среднюю 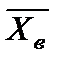, выборочную дисперсию 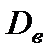,выборочное среднее квадратическое отклонение .

Решение

;

;

.

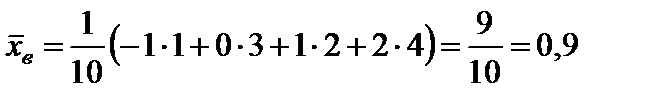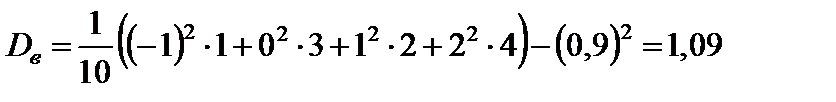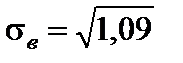Тест 7. 12. Для вариационного ряда

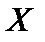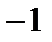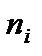выборочное среднее 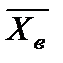, выборочная дисперсия 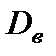равны:

1) , ;

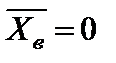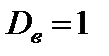2) , ;

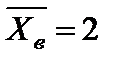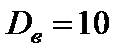3) , ;

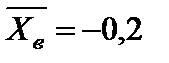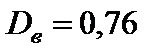4) , .

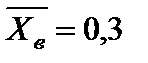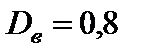Коэффициент вариации 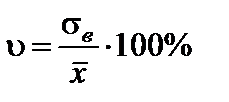характеризует относительное значение среднего квадратического отклонения и служит для сравнения колеблемости несоизмеримых показателей.

Обобщающими характеристиками выборочных распределений являются моменты вариационного ряда.

Начальным выборочным моментом т-го порядка (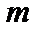 =0,1,2,…) называется величина 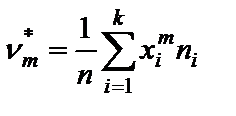, где 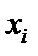– наблюденное значение с частотой 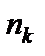, 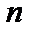– число наблюдений, 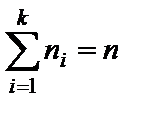. Очевидно, что 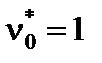, , 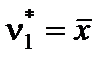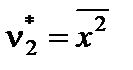и т. д.

Центральным выборочным моментом т-го порядка (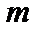 =0,1,2,…) называется величина 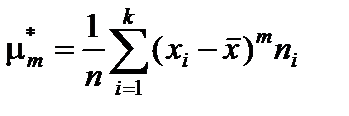, где 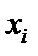– наблюденное значение с частотой 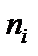, 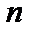– число наблюдений, 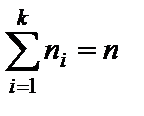, 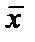– выборочное среднее. Очевидно, что , , ,

, .

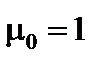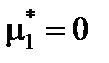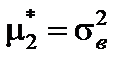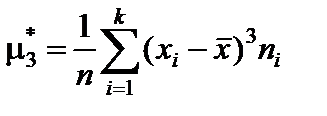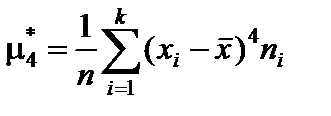Важную роль при исследовании статистических совокупностей играют асимметрия и эксцесс распределения признака, которые вычисляются соответственно по формулам: , .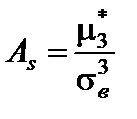

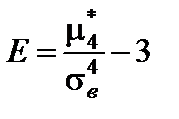Если кривая распределения симметрично относительно прямой 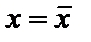, то распределение симметрично. Тогда 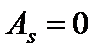(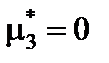). При асимметричном распределении вершина кривой сдвинута относительно ординаты выборочной средней. Если 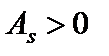, то асимметрия правосторонняя или положительная (рис. 18а), если , то левосторонняя или отрицательная (рис. 18б).

а) б)

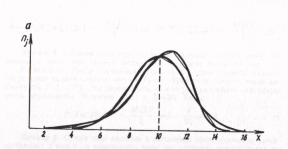
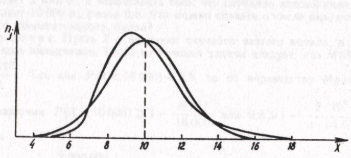
Рис. 18. Правосторонняя (а) и левосторонняя (б) асимметричность