Контрольная работа №4
Теория функций комплексного переменного.
Уравнения математической физики
Теория вероятности
Математическая статистика
Введение.
Общий курс высшей математики, изучаемой студентами-заочниками инженерно-технических и технологических специальностей, состоит из аналитической геометрии с элементами линейной алгебры, математического анализа, элементов теории вероятности и математической статистики.
Этот курс ставит основной своей задачей сообщить студенту сведения о высшей математике, необходимые для успешного изучения общетеоретических и специальных дисциплин, и также развить навыки логического мышления.
Учебный материал по курсу высшей математики распределен на пять первых семестров. В конце каждого семестра предусмотрен зачет или экзамен по изученным разделам математики. Соответственно этим разделам студенты выполняют контрольные работы согласно учебному плану своей специальности.
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом. Лекции, практические, индивидуальные межсессионные занятия призваны помочь им в самостоятельной работе и выполнении контрольных работ.
Работа студента-заочника над учебным материалом по математики состоит из следующих элементов: слушание лекций, участие в практических занятиях, участие в межсессионных индивидуальных занятиях, изучение материала по учебникам, решение задач, ответы на вопросы для самоконтроля, выполнение контрольных работ (1-5 в семестр), сдача зачетов и экзаменов.
Настоящий сборник содержит все задания для выполнения контрольных работ по высшей математике а также ставит цель помочь студенту-заочнику самостоятельно работать над учебным материалом по высшей математике, в нем перечислена литература, рекомендованная для самостоятельного изучения материала, содержится программа по всему курсу, методика изучения и решения типовых вариантов контрольных работ.
Требования к оформлению контрольных работ
Контрольная работа должна выполняться студентом в соответствии с номером варианта, который определяется двумя последними цифрами номера зачетной книжки студента.
При оформлении контрольной работы необходимо учитывать следующие требования:
1) на титульном листе указать номер варианта;
2) контрольные работы оформлять, оставляя поля для замечаний преподавателя;
3) условия задач необходимо записывать полностью. Если задание имеет общую формулировку, его условие необходимо переписать, подставляя числовые значения, соответствующие номеру варианта;
4) решения заданий оформлять аккуратно, приводить достаточное количество пояснений, делать необходимые рисунки.
Контрольную работу необходимо сдать за 10 дней до начала экзаменационной сессии, в противном случае студент не будет допущен до зачета или экзамена.
Решение типового варианта
Пример 1. Указать область, определяемую условиями 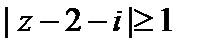 ,
, 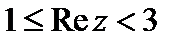 ,
, 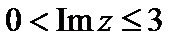 .
.
Решение. Неравенство 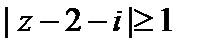 , равносильное неравенству
, равносильное неравенству 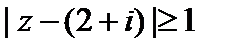 , определяет внешность круга (включая границу) радиусом 1 с центром в точке
, определяет внешность круга (включая границу) радиусом 1 с центром в точке 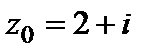 . Неравенство
. Неравенство 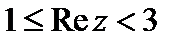 или
или 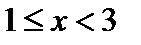 определяет полосу, заключенную между прямыми
определяет полосу, заключенную между прямыми 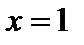 и
и 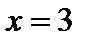 . Неравенство
. Неравенство 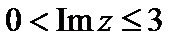 или
или 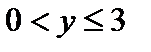 определяет полосу, заключенную между прямыми
определяет полосу, заключенную между прямыми 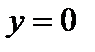 и
и 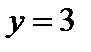 .
.
Пример 2. Найти аналитическую функцию 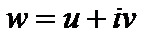 по ее заданной действительной части
по ее заданной действительной части 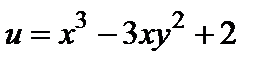 .
.
| . |
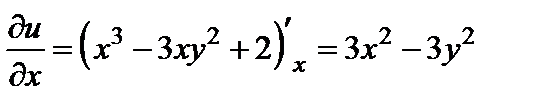 , то согласно первому условию
, то согласно первому условию 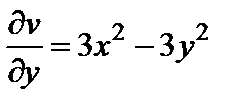 . Отсюда, интегрируя по y, находим:
. Отсюда, интегрируя по y, находим:
Для определения функции 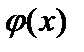 воспользуемся вторым условием Коши-Римана. Так как
воспользуемся вторым условием Коши-Римана. Так как 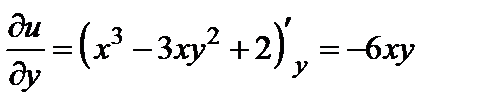 , а
, а 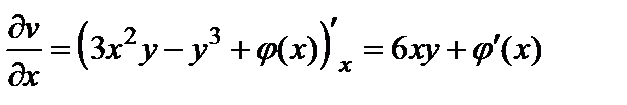 , то
, то 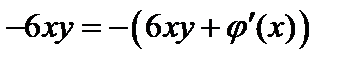 . Отсюда
. Отсюда 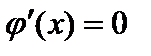 и
и 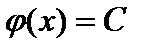 , где
, где 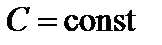 . Поэтому
. Поэтому 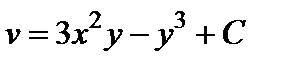 . Находим функцию
. Находим функцию 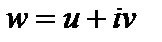 :
:
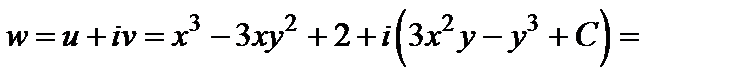
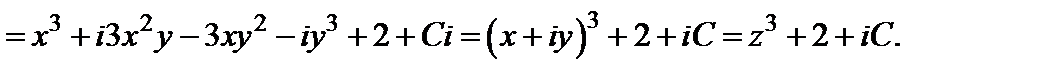
Пример 3. Решить задачу Коши
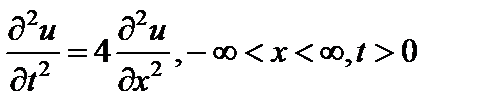 ,
,
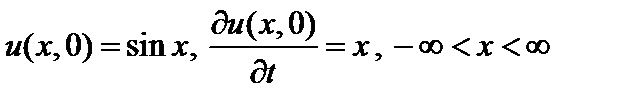 .
.
Решение. По условию 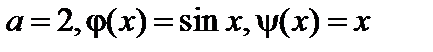 , поэтому, пользуясь формулой
, поэтому, пользуясь формулой 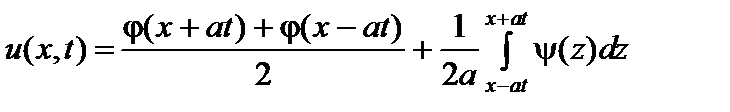 , получим
, получим
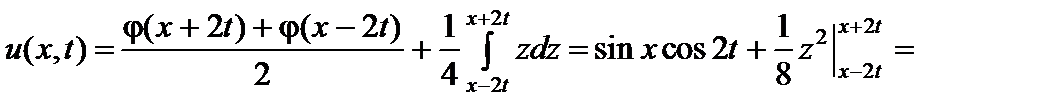

Пример 4. Дан тонкий однородный стержень длиной 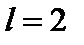 , изолированный от внешнего пространства, начальная температура которого равна
, изолированный от внешнего пространства, начальная температура которого равна 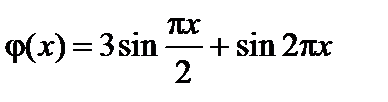 . Концы стержня поддерживаются при температуре, равной нулю. Определить температуру стержня в момент
. Концы стержня поддерживаются при температуре, равной нулю. Определить температуру стержня в момент 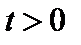 .
.
Решение. Математически данная задача сводится к решению следующей смешанной задачи для одномерного однородного уравнения теплопроводности:
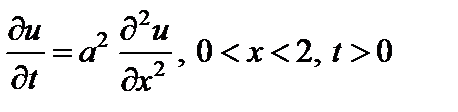 ,
,
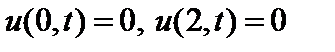 ,
,
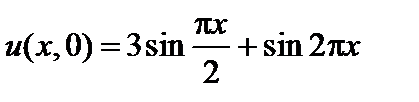 ,
,
решение которой дается формулой 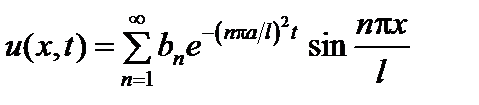 , где
, где 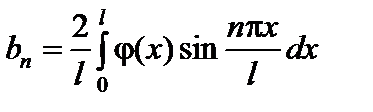 при
при  . Вычислим
. Вычислим  :
:
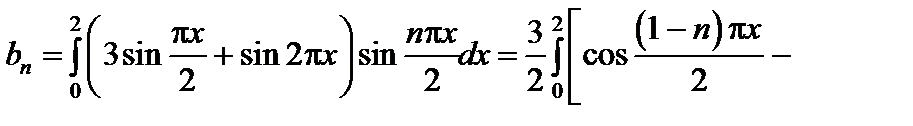
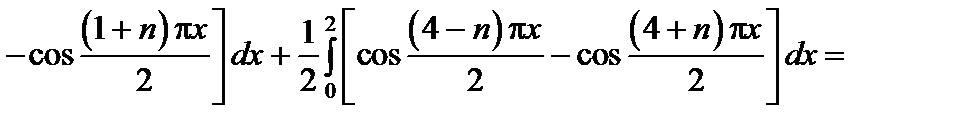
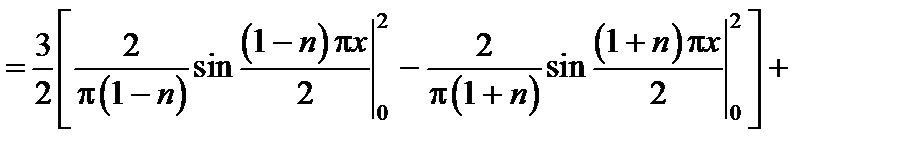
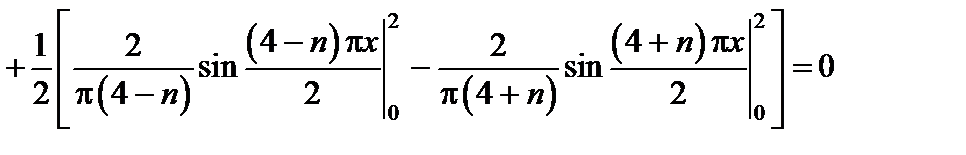 ,
,
при 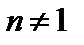 и
и 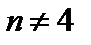 . Если
. Если 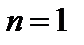 и
и 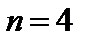 , получим
, получим
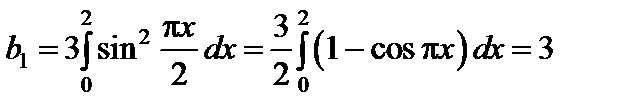 ,
,
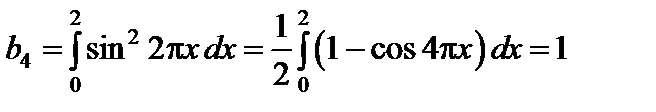 .
.
Замечание. К оэффициенты 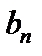 можно определить из тождества
можно определить из тождества
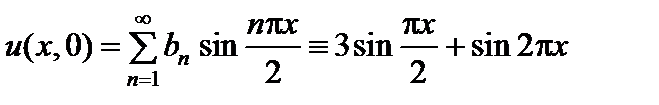 .
.
Отсюда в силу линейной независимости системы функций 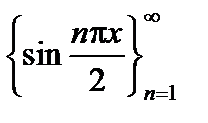 получим
получим 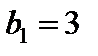 ,
, 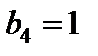 ,
, 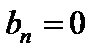 для
для  .
.
Пример 5. Найти решение уравнения Лапласа в области, заключенной между двумя концентрическими окружностями радиусов 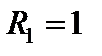 и
и  с центрами в начале координат, удовлетворяющее граничным условиям
с центрами в начале координат, удовлетворяющее граничным условиям 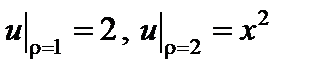 .
.
Решение. Запишем граничные условия в полярных координатах: первое не изменится, второе примет вид
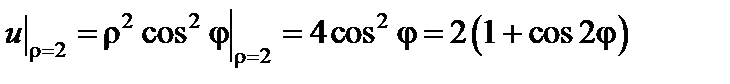 .
.
Решение задачи ищем в виде 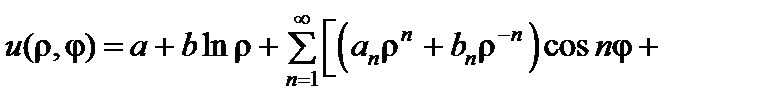
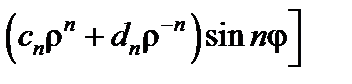 . Удовлетворим граничным условиям:
. Удовлетворим граничным условиям:
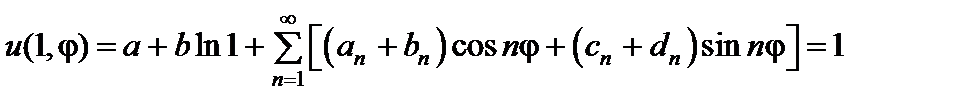 ,
,
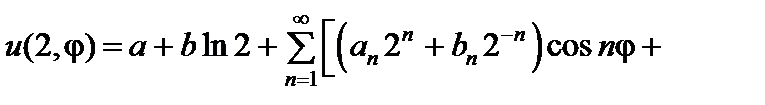
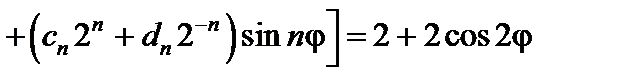 .
.
Отсюда
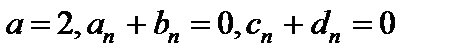 для
для 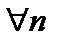 ;
;
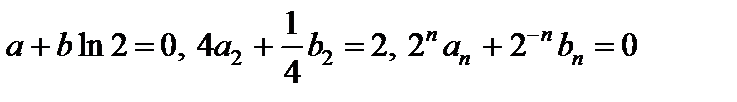 для
для 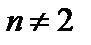 ,
,
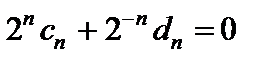 для
для 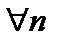 .
.
З этих двух серий соотношений (линейной алгебраической системы уравнений) определяем коэффициенты:
а) 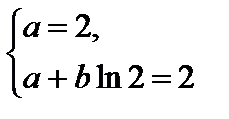
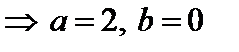 ,
,
б) 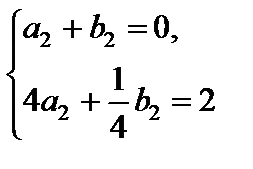
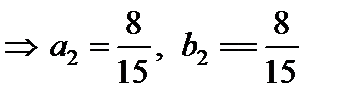 ,
,
в) все остальные коэффициенты равны нулю.
Итак,
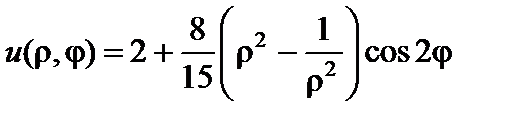 ,
,
или в декартовых координатах 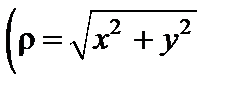 ,
, 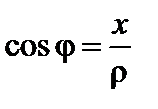 ,
, 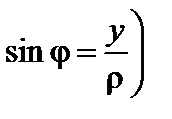
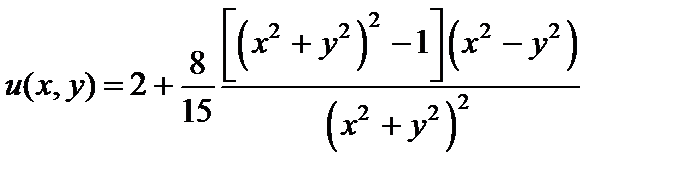 .
.
Задача 5.1. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди шести взятых наудачу деталей 4 стандартных (событие 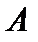 ).
).
Решение. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т. е. числу сочетаний из 10 элементов по 6 элементов: 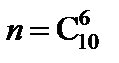 .
.
Определим число исходов, благоприятствующих событию А. Четыре стандартные детали можно взять из семи стандартных деталей 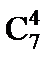 способами. Остальные 6-4=2 детали должны быть нестандартными. Их можно взять из 10-7=3 нестандартных деталей
способами. Остальные 6-4=2 детали должны быть нестандартными. Их можно взять из 10-7=3 нестандартных деталей 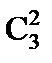 способами. Таким образом, число благоприятствующих исходов равно
способами. Таким образом, число благоприятствующих исходов равно 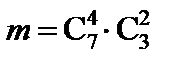 .
.
Следовательно, искомая вероятность равна
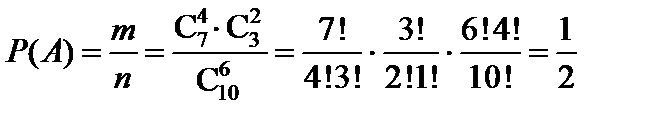 .
.
 2015-04-20
2015-04-20 536
536








