2015-04-20
547
а) Определим параметр с из условия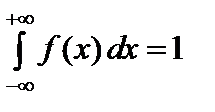 
:
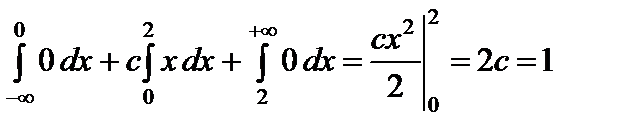, т е. 
.
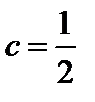б) Найдем функцию распределения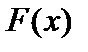 
:
1) если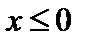 
, то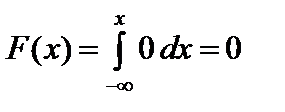 
;
2) если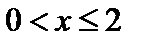 
, то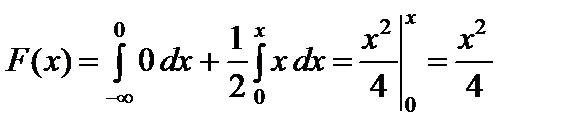 
;
3) если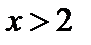 
, то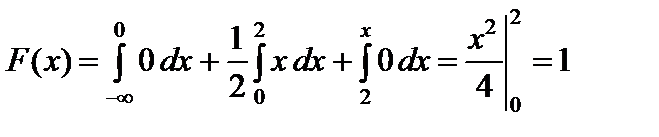 
.
Следовательно
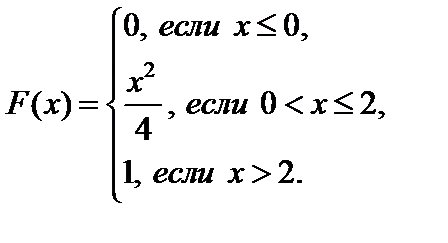
в)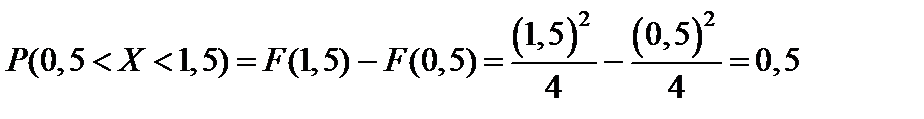 
г)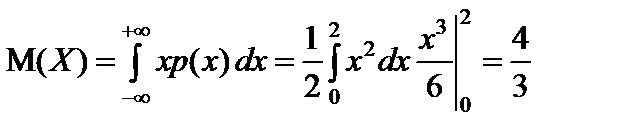 
;
;
.
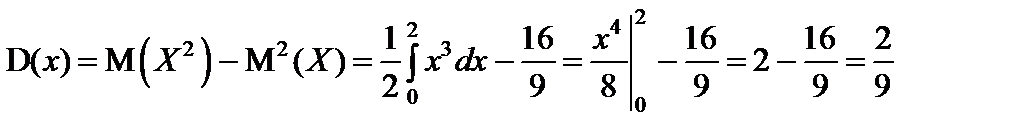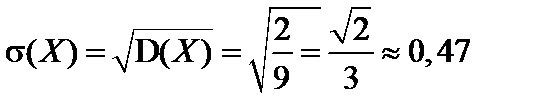Задача 8. Случайная величина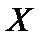 
имеет нормальное распределение с выборочным средним 
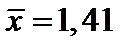и средним квадратическим отклонением 
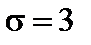. Найти доверительные интервалы для оценки неизвестного математического ожидания 
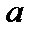, если объем выборки 
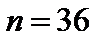и задана надежность (доверительная вероятность) оценки 
.
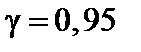Решение. Воспользуемся рабочей формулой
,
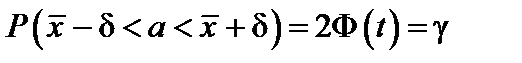где точность оценки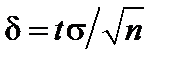 
.
По таблице функции Лапласа (см. приложение) из соотношения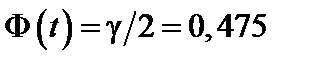 
найдем 
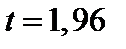. Определим точность оценки
.
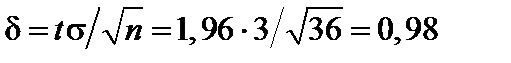Следовательно, доверительный интервал будет
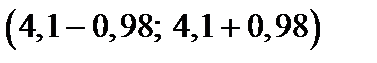т. е.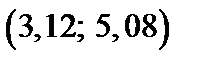 
.
Отв.: .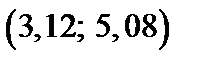
Замечание. Так как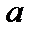 
– постоянная величина, то было бы ошибочным написать 
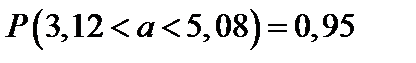, ибо либо 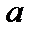заключена в этом интервале (тогда событие 
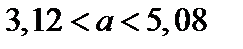достоверно и вероятность равна единице), либо нет (это событие невозможно, вероятность его равна нулю).
Надежность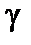 
указывает, сто если произведено достаточное число выборок, то 95% из них определяет такие доверительные интервалы, в которых параметр действительно заключен; лишь в 5% случаев он может выйти за границы доверительного интервала.
