Построение математической модели задачи

Обозначим через x_j количество единиц продукции j -го вида, планируемое к выпуску (j =1,..., п). Тогда суммарная прибыль f(х₁,..., х_n) от реализации выпущенной предприятием продукции при плане производства (x₁;...;х_n) может быть представлена следующей функцией:

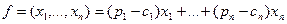
или в компактной форме:

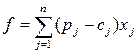. (2.1)

При этом общий фактический расход i- го ресурса, затрачиваемый на производство ассортимента продукции в запланированном объеме, представим в виде суммы:

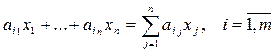
и не должен превышать имеющегося запаса b_i, т.е.:

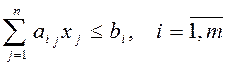. (2.2)

Ограничения на объемы отдельных видов выпускаемой продукции (обусловлены соотношениями спроса-предложения или другими технико-экономическими и управленческими условиями) можно записать, исходя из смысла нижней и верхней их границ, с помощью системы неравенств:

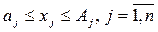. (2.3)

Итак, математически задача сводится к нахождению числовых значений переменных x₁,..., х_n, удовлетворяющих линейным ограничениям (2.2), (2.3) и доставляющих максимум линейной функции (2.1). Соотношения (2.1) — (2.3) — математическая модель данной задачи, т.е. математическая модель исходной задачи будет иметь вид:

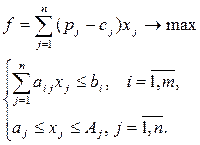(2.4)

Количество ресурсов m, их запас b_i, количество переменных п, коэффициенты 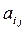, c_j, р_j, а_j, А_j определяются непосредственно из условия задачи. Рассмотрим несколько типичных примеров задач из данной группы.

Пример 2.1 Задача об использовании сырья

Небольшая фабрика изготовляет два вида красок: для наружных (Е) и внутренних (I) работ. Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта А и В. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 тонн соответственно. Расходы продуктов А и В на 1 тонну соответствующих красок приведены в таблице:

Исходный продукт	Расход исходных продуктов (в тоннах) на 1 тонну краски	Максимально возможный запас продукта, тонн
краска Е	краска I
А
В

Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает величину спроса на краску Е более чем на 1 тонну. Кроме того, установлено, что спрос на краску I никогда не превышает 2 тонн в сутки. Оптовые цены одной тонны красок равны: 3 тыс. грн. для краски Е, 2 тыс. грн. для краски I.

Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?

Переменные модели.

Так как нужно определить объемы производства краски каждого вида, переменными в модели являются:

Х₁ – суточный объем производства краски Е (в тоннах);

Х₂ – суточный объем производства краски I (в тоннах).

Целевая функция модели.

Так как стоимость 1 тонны краски Е равна 3 тыс. грн., суточный доход от ее продажи в количестве Х₁ тонн составит 3Х₁ тыс. грн. Аналогично доход от реализации Х₂ тонн краски I составит 2Х₂ тыс. грн. в сутки. При допущении независимости объемов сбыта каждой из красок общий доход равен сумме двух слагаемых – дохода от продажи краски Е и дохода от продажи краски I.

Обозначив общий доход (в тыс. грн.) через F, можно дать следующую математическую формулировку целевой функции: определить значения (допустимые) Х₁ и Х₂, максимизирующие величину общего дохода:

F = 3Х₁ + 2Х₂.

Ограничения модели.

При решении рассматриваемой задачи должны быть учтены ограничения на расход исходных продуктов, а также отражены соотношения спроса на изготовляемые краски.

Ограничения на расход исходных продуктов можно записать следующим образом:

Фактический расход исходного продукта для производства обоих видов красок

Максимально возможный запас данного исходного продукта

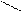
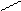Это приводит к следующим двум ограничениям:

Х₁ + 2Х₂ £ 6 (для А),

2Х₁ + Х₂ £ 8 (для В).

Ограничения, моделирующие соотношения спроса на продукцию, имеют следующий смысл:

Математически эти ограничения записываются следующим образом:

Х₂ - Х₁ £ 1 (соотношение величин спроса на краску I и краску Е),

Х₂ £ 2 (максимальная величина спроса на краску I).

Неявное (т.е. «подразумеваемое») ограничение заключается в том, что объемы производства продукции не могут принимать отрицательных значений. Чтобы предотвратить получение таких недопустимых решений, потребуем выполнения условия неотрицательности переменных, т.е. введем ограничения на их знак:

Х₁ ³ 0 (объем производства краски Е),

Х₂ ³ 0 (объем производства краски I).

Итак, математическую модель можно записать в следующем виде:

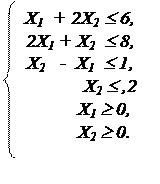Определить суточные объемы производства (Х₁ и Х₂) краски Е и краски I (в тоннах), при которых достигается max F = 3Х₁ + 2Х₂ (целевая функция), при ограничениях:

Пример 2.2 Задача об ассортименте продукции

Пусть фирма выпускает три вида продукции. В процессе производства используется три технологических операции. Технологическая схема производства изделий видов 1, 2, 3 показана на рисунке:

Так как эти технологические операции используются фирмой и для других производственных целей, фонд рабочего времени, в течение которого операции 1, 2 и 3 могут быть применены для производства рассматриваемых изделий, ограничен предельными значениями (в сутки):

· для 1-й операции – 430 минут;

· для 2-й операции – 460 минут;

· для 3-й операции – 420 минут;

Изучение рынка сбыта показало, что ожидаемая прибыль от продажи одного изделия видов 1, 2, 3 составляет 3, 2 и 5 грн. соответственно.

Каков наиболее выгодный суточный объем производства каждого вида продукции?

Словесная формулировка задачи. Для данной фирмы требуется определить суточные объемы производства изделий каждого вида, при которых максимизируется общая прибыль, при условии, что время использования каждой технологической операции, в течение суток, не превышает соответствующего предельного значения.

Переменные модели.

Х₁ – количество изделий вида 1,

Х₂ – количество изделий вида 2,

Х₃ - количество изделий вида 3.

Целевая функция модели.

Так как ожидаемая прибыль от продажи одного изделия каждого вида равна соответственно 3, 2 и 5 грн., а их количество равно соответственно Х_1, Х₂ и Х₃ штук, то величина прибыли, получаемая от реализации планируемого количества изделий каждого вида, равна соответственно 3Х₁, 2Х₂ и 5Х₃ грн. Тогда общая прибыль составит:

F = 3Х₁ + 2Х₂ + 5Х₃

Ограничения модели.

Система ограничений должна отражать условия непревышения времени использования технологических операций 1, 2 и 3 свыше предельного суточного значения.

Для операции 1:

- для изделия 1 ^го вида операция 1 длится 1 мин, следовательно, Х₁ шт. изделий 1 ^го вида потребуют времени 1*Х₁ минут;

- для изделия 2 ^го вида операция 1 длится 2 мин, следовательно, Х₂ шт. изделий 2 ^го вида потребуют времени 2*Х₂ минут;

- для изделия 3 ^го вида операция 1 длится 1 мин, следовательно, Х₃ шт. изделий 3 ^го вида потребуют времени 1*Х₃ минут.

Общее время, которое используется для производства изделий трех видов при выполнении операции 1 равно Х₁ + 2Х₂ + Х₃ минут. Это время не должно превышать по условию 430 минут. Таким образом, математически это можно записать в следующем виде:

Х₁ + 2Х₂ + Х₃ £ 430.

Аналогичны рассуждения для 2-й и 3-й операций. В результате получаем для них:

3Х₁ + 0*Х₂ + 2Х₃ £ 460,

Х₁ + 4Х₂ + 0*Х₃ £ 420.

На переменные также накладываются условия неотрицательности, т.е.

Х₁ ³ 0, Х₂ ³ 0, Х₃ ³ 0.

Итак, математическую модель можно записать в следующем виде:

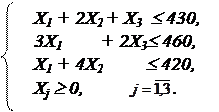Определить суточные объемы производства изделий 3-х видов Х₁, Х₂, Х₃, при которых достигается max F = 3Х₁ + 2Х₂ + 5Х₃, при ограничениях:

Если выпускаемая продукция используется в дальнейшем, то ее возможно придется выпускать в определенных пропорциях. И в этом случае модель дополняется условиями комплектности. Могут быть и другие ограничения.

В обобщенной задаче оптимального производственного планирования мы предполагали, что все 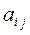и с_j являются постоянными величинами, что может не соответствовать действительному положению дел. В реальном производстве не исключается возможность появления брака, доля которого может увеличиваться с ростом интенсивности производства. Предположим, в условиях рассматриваемого предприятия установлено, что из-за наличия брака расход ресурсов на изготовление продукции связан с объемом x_j ее производства и приближенно выражается функцией:

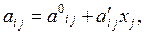
где 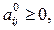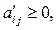(i=1,…,m; j=1,…n).

Вместе с этим и себестоимость с_j продукции зависит от объема производства и в первом приближении описывается функцией вида:

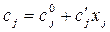
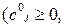
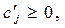
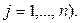
Подставляя данные выражения в (2.1) и (2.2), получаем:

.

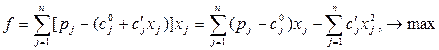
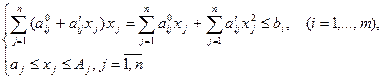Как видно из последних соотношений модель становится нелинейной.