Довольно обширный класс задач математического программирования образуют так называемые задачи на составление смесей или задачи на использование заменителей. Задача подобного рода возникает в случае необходимости смешивания различных компонент со сходными свойствами с целью создания смеси, отвечающей определенным требованиям, или при необходимости замены в смеси одних компонент другими. Характерный пример такой задачи — составление наиболее экономичных смесей горючего для двигателей разных типов. Известно, что выпускаемые марки бензина различаются теплотворной способностью, температурой воспламенения, степенью очистки и т.п. Возникает задача составления наиболее дешевой смеси из различных марок бензина при условии, чтобы определенные количественные показатели смеси были выше (или ниже) заранее установленных величин. Аналогичной является задача на составление наиболее дешевой смеси различных сортов угля для нагрева паровых котлов и т.п.
Не менее важными являются задачи составления экономной шихты для выплавки чугуна и стали. Так, для получения легированной стали необходимо использовать шихту определенного химического состава. Многие ингредиенты шихты весьма дорогостоящие, и вместе с тем в ее состав входят малоценные материалы — чугун, лом, отходы с определенным известным содержанием присадок. Возникает задача выбора шихты минимальной стоимости, в состав которой должны входить в заданных количествах необходимые химические вещества.
К задачам на составление смесей относится также определенный тип задач на использование заменителей. Например, проблема замены одних средств производства другими с целью достижения оптимального эффекта производства.
Задачи на смеси приходится решать при определении рациональных норм потребления продуктов питания и в связи с этим при составлении перспективного плана развития пищевой промышленности или при планировании централизованного снабжения продуктами питания детских учреждений, спортивных и оздоровительных лагерей, больниц, войсковых частей и т.д. Встречаются подобные задачи и в сельскохозяйственной практике, например, при выборе оптимального рациона для откорма скота. В простейшей постановке эта задача формулируется следующим образом.
Пусть хозяйство располагает п видами кормов (сено, силос, концентраты и т.д.), каждый из которых содержит в различных пропорциях m видов питательных веществ (белки, кальций, фосфор, витамины и др.). Известно, что в единице корма j -го (j =1,..., n). вида содержится аij единиц i -го питательного вещества (i =1,..., m). Минимальная суточная потребность в i -ом питательном веществе составляет bi единиц, себестоимость производства единицы корма j -го вида равна cj, а выделяемый суточный объем ограничен величиной aj. Требуется выбрать рацион — набор и количество кормов — так, чтобы количество каждого питательного вещества было не меньше требуемого, а суммарная стоимость рациона была минимальной.
Построим математическую модель данной задачи.
Обозначим через xj (j =1,... n) количество единиц корма j -го вида, включаемого в суточный рацион. Тогда общее количество i -го питательного вещества, содержащегося в рационе (х1;...; хn), выразится суммой:
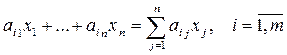 .
.
Эта сумма не должна быть меньше нужного минимума bi по всем видам питательных веществ, что математически выразится следующей системой неравенств:
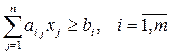 .
.
С другой стороны, суточное потребление каждого корма ограничено имеющимися запасами ai. Отсюда дополнительные условия на компоненты рациона: 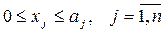 .
.
Суммарная стоимость кормов, составляющих суточный рацион, определится выражением:
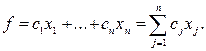
Таким образом, оптимальным рационом будет такой набор (х1;...; хn) кормов, который обращает в минимум линейную функцию f при соблюдении ограничений, а математическая модель задачи о рационе будет иметь вид:
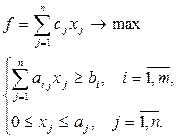
Если учесть обусловленное зоотехническими требованиями определенное соотношение в рационе объемов сочных и грубых кормов, то придется дополнить модель соответствующими ограничениями. Чтобы обеспечить разнообразие рациона, следует иметь в наличии не менее а0j единиц j -го вида корма, а в модель задачи придется включить условия:
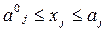 .
.
Иногда приходится учитывать ограничения сверху (величиной 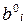 ) на потребление некоторых питательных веществ. Тогда необходима модификация одного из условия системы ограничений модели, а именно следует рассматривать ограничения вида:
) на потребление некоторых питательных веществ. Тогда необходима модификация одного из условия системы ограничений модели, а именно следует рассматривать ограничения вида:
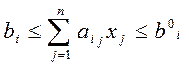 .
.
В итоге математическая модель задачи о рационе примет обобщенный вид:
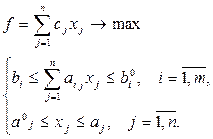
Пример 2.3 Задача о рационе
При откорме каждое животное ежедневно должно получить не менее 60 единиц питательного вещества А, не менее 50 ед. вещества В. Указанные питательные вещества содержат три вида корма. Содержание единиц питательных веществ в 1 кг каждого из видов кормов приведено в таблице:
| Тип вещества | Кол-во единиц питательных веществ в 1 кг корма вида | ||
| І | ІІ | ІІІ | |
| А | |||
| В |
Составить дневной рацион, обеспечивающий получение необходимого количества питательных веществ при минимальных денежных затратах, если цена 1 кг корма 1 го вида составляет 19 грн., корма 2 го вида – 24 грн., корма 3 го вида – 25 грн.
Построим математическую модель задачи. Пусть Хi – количество корма i го вида, включаемого в дневной рацион животных, i = 1, 2, 3.
Целевая функция задачи выражает суммарные денежные затраты на составление рациона, которые должны быть минимальными:
F = 19X1 + 24X2 + 25X3 ® min
На переменные задачи накладываются ограничения на количественное содержание питательных веществ А и В в дневном рационе животного.
для вещества А: X1 + 3X2 + 4X3 ³ 60,
для вещества В: 2X1 + 4X2 + 2X3 ³ 50.
Левая часть каждого из ограничений формально выражает то количество единиц соответствующего питательного вещества, которое животное фактически получит в результате составления некоторого рациона Х=(Х1, Х2, Х3). Правая же часть того же ограничения – это требуемое количество единиц соответствующего питательного вещества. Учитывая требование условия задачи: животное должно получить необходимое количество единиц питательных веществ, выбираем знак неравенств “³”.
Кроме того, значения переменных Хi, i = 1, 2, 3, не могут принимать отрицательные значения, т.е. Хi ³ 0, i = 1, 2, 3.
Таким образом, математическая модель исходной задачи будет иметь вид:
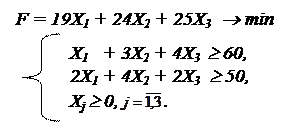
 2015-04-30
2015-04-30 7806
7806








