Задача о раскрое материалов

На раскрой (распил, обработку) поступает материал одного образца в количестве а единиц. Требуется изготовитьиз него l разных комплектующих изделий в количествах, пропорциональных числам 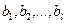(условие комплектности). Каждая единица материала может быть раскроена n различными способами, причем использование i-го способа (i =1,2,..., п) дает а_ik единиц k -го изделия (k = 1,2,..., l;).

Необходимо найти план раскроя, обеспечивающий максимальное число комплектов.

Составим экономико-математическую модель задачи. Обозначим, xi — число единиц материала, раскраиваемых i -м способом, и х — число изготавливаемых комплектов изделий. Так как общее количество материала равно сумме его единиц, раскраиваемых различными способами, то .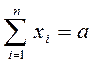

Требование комплектности выразится уравнениями:

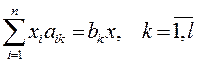Очевидно, что должны соблюдаться условия:

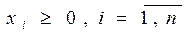Экономико-математическая модель задачи: найти такое решение Х=(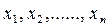), удовлетворяющее построенной системе уравнений и условию неотрицательности переменных, при котором функция F=х принимает максимальное значение, т.е.:

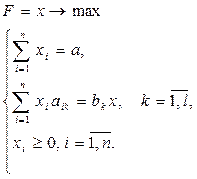
Пример 2.4

Для изготовления брусьев длиной 1,2 м, 3 м и 5 м в соотношении 2:1:3 на распил поступают 195 бревен длиной 6 м. Определить план распила, обеспечивающий максимальное число комплектов. Составить экономико-математическую модель задачи.

Построение математической модели.

Прежде всего определим всевозможные способы распила бревен, указав соответствующее число получаемых при этом брусьев:

Способ распила i	Число получаемых брусьев длиной, м
1,2	3,0	5,0
		-	-
			-
	-		-
	-	-

Обозначим: 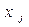— число бревен, распиленных i -м способом(i =1, 2, 3, 4); х — число комплектов брусьев.

Учитывая, что все бревна должны быть распилены, а число брусьев каждого размера должно удовлетворять условию комплектности, экономико-математическая модель задачи примет вид (согласно приведенной выше обобщенной форме записи математической модели задачи о раскрое материала):

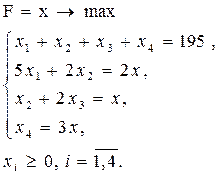
Задачу о раскрое легко обобщить на случаи т раскраиваемых материалов.

Пусть каждая единица j-го материала (j = 1, 2,..., т) можетбыть раскроена п различными способами, причем использование i-го способа (i = 1, 2,..., n) дает 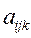единиц k-го изделия (k = 1, 2,..., l ), a запас j-го материала равен 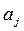единиц.

Обозначим 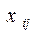— число единиц j-го материала, раскрываемого i-м способом.

Экономико-математическая модель задачи о раскрое в общей постановке примет вид: найти такое решение Х=(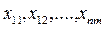), удовлетворяющее системе

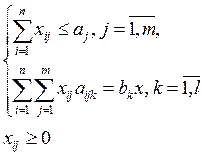
и условию 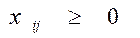, при котором функция F = х принимает максимальное значение.

Пример 2.5

Продукция бумажной фирмы выпускается в виде бумажных рулонов стандартной ширины – по 20 м. По специальным заказам потребителей фирма поставляет рулоны и других размеров, для чего производится разрезание стандартных рулонов. Типичные заказы на рулоны нестандартных размеров приведены в таблице:

ЗАКАЗ	Требуемая ширина, м.	Требуемое количество рулонов

Специализированные заказы выполняются на разрезном устройстве, режущая кромка которого устанавливается в требуемом положении, причем рулон может быть разрезан несколькими способами. Варианты раскроя не должны давать рулонов – остатков шириной более 4 м.

Требуется найти сочетание вариантов установки режущей кромки, при котором поступившие заказы удовлетворяются с минимальными потерями.

Переменные.

Требуемая ширина, м.	Вариант установки режущей кромки	Минимальное количество рулонов




Потери на 1 м длины

Пусть X_j – количество стандартных рулонов, разрезаемых по варианту j, .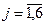

Целевая функция. Общие потери бумаги на 1 м длины:

F = 4Х₁ + 3Х₂ + Х₃+ Х₅ + 2Х₆

Ограничения. Ограничения непосредственно связаны с требованием обеспечить изготовление заказанного количества нестандартных рулонов. Если будут использованы все приведенные в таблице варианты раскроя стандартного рулона, то мы получим следующие результаты:

Количество рулонов шириной 5 м: 2Х₂ + 2Х₃ + 4Х₄ + Х₅.

Количество рулонов шириной 7 м: Х₁ + Х₂ + 2Х_5.

Количество рулонов шириной 9 м: Х₁ + Х₃ + 2Х₆.

Каждое из этих соотношений определяет количество фактически полученных нестандартных рулонов, которое должно быть не меньше 150, 200, 300 для рулонов 5, 7 и 9 м соответственно.

На переменные задачи накладываются еще ограничения неотрицательности.

Итак, математическая модель в общем виде запишется:

min F = 4Х₁ + 3Х₂+ Х₃+ Х₅+ 2Х₆, при ограничениях

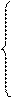2Х₂ + 2Х₃+ 4Х₄+ Х₅ ³ 150

Х₁ + Х₂+ 2Х₅³ 200

Х₁ + Х₃ + 2Х₆³ 300

Х_j ³ 0,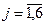

Рассмотрим модификацию или, в некотором смысле, обобщение предыдущих задач на следующем примере.

Пример 2.6

Имеется три технологических процесса для выделения из руды двух нужных веществ А и В. Из каждой тонны руды при применении процессов I, II и III получается, соответственно, 0,4 и 0,6; 0,6 и 0,5; 0,2 и 0,2 килограммов вещества А и В, и при этом затраты составляют: 5 тыс. грн. для процесса I, 6 тыс. грн., для процесса II и 1 тыс. грн., для процесса III. Определить оптимальное распределение 10 т руды по процессам I, II и III, минимизирующее затраты, если необходимо получить не менее 4 кг каждого вещества.

Переменные.

Пусть X_j – количество тонн руды, направляемых на переработку по j-му процессу,. .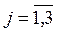

Целевая функция. Целью данной задачи является минимизация суммарных затрат на применение трех технологических процессов по переработке руды. Учитывая затраты на переработку 1 тонны руды по каждому из процессов и план переработки руды, т.е. планируемое распределение руды, суммарные затраты можно выразить функцией:

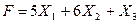Ограничения. В рассматриваемом примере существенными являются три ограничения на допустимые значения переменных модели:

1. Условие распределения 10 тонн руды между технологическими процессами переработки: .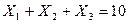

2. Условия выделения из руды минимального количества веществ А и В:

- для вещества А: ;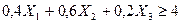

- для вещества В: .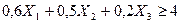

3. Условие неотрицательности переменных модели: .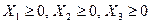

Таким образом, математическая модель исходной задачи будет иметь вид:

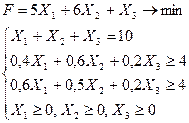
2.5 Задача об оптимальном плане перевозок

Эту задачу часто называют транспортной. В простейшем варианте транспортная задача возникает при необходимости наиболее рациональной перевозки некоторого однородного груза. При этом потребителям безразлично, из каких пунктов он поступает, лишь бы был удовлетворен спрос, а каждый поставщик имеет возможность доставлять груз любому потребителю. Обратные перевозки не предусматриваются. Итак, пусть в m пунктах производится соответственно a₁,…,a_m единиц некоторого продукта, потребности в котором в n пунктах выражаются величинами b₁,…,b_n единиц (предполагается, что общий спрос на продукт не превышает возможностей производства, т. е. ).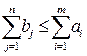

Известны затраты c_ij по перевозке единицы продукта из i -го пункта производства в j -й пункт потребления. Требуется составить наиболее экономный план перевозок (в смысле суммарных транспортных расходов), обеспечивающий удовлетворение всех потребностей в продукте.

Построим математическую модель данной задачи.

Обозначим через х_ij количество продукта, перевозимого из i -го пункта производства в j- й пункт потребления. Тогда задача сводится к определению числовых значений mn неизвестных х_ij (i=1,..., m; j=1,..., n), удовлетворяющих условиям:

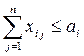
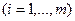
(из каждого пункта производства вывозится не более производимого в нем количества продукта);

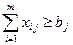
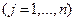
(в каждый пункт потребления доставляется не менее требуемого им количества продукта);

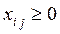(i=1,..., m; j=1,..., n) (перевозимое количество продукта обратно в пункт производства не возвращается) и доставляющих минимум функции 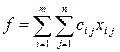(суммарные затраты на перевозки продукта).