С каждой задачей линейного программирования связывается другая задача тоже линейного программирования, которая называется двойственной задачей (или сопряженной) по отношению к исходной задаче, которая называется прямой.
Двойственная задача строится по отношению к прямой задаче, записанной в стандартной форме:
F=c1x1+c2x2+…+cnxn ® max (3.21)
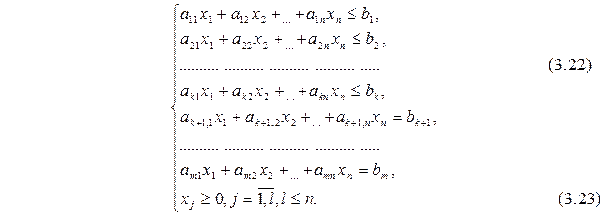
Задача, состоящая в нахождении минимального значения функции:
L = b1y1 + b2y2 + … + bmym (3.24)
при условиях:
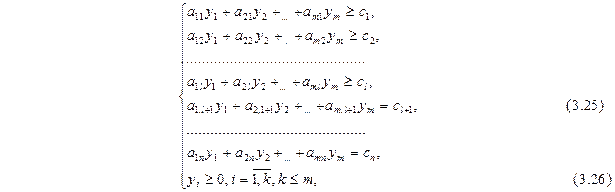
называется двойственной по отношению к задаче (3.21) – (3.23).
Правила построения двойственной задачи приведены в таблице:
| Структурные характеристики ЗЛП | Задача линейного программирования | |
| Прямая | Двойственная | |
| 1.Целевая функция | Максимизация (max) | Минимизация (min) |
| 2.Количество переменных | n переменных | Равно количеству ограничений прямой задачи (3.22), yi, 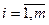 т.е. m т.е. m
|
| 3.Количество ограничений | m ограничений 
| Равно количеству переменных прямой задачи xj, 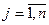 , т.е n , т.е n
|
| 4.Матрица коэффициентов в системе ограничений | 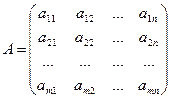
| 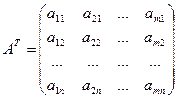
|
| 5.Коэффициенты при переменных в целевой функции | c1,c2,…,cn | b1,b2,…,bm |
| 6.Правая часть системы ограничений | b1,b2,…,bm | c1,c2,…,cn |
| 7.Знаки в системе ограничений | а) xj ≥ 0- условие неотрицательности | j -е ограничение имеет знак «≥» |
| б) на переменную xj не наложено условие неотрицательности | j- е ограничение имеет знак «=» | |
| в) i -е ограничение имеет знак «≤» | переменная yi ≥0 | |
| г) i -е ограничение имеет знак «=» | на переменную yi не наложено условие неотрицательности |
 2015-04-30
2015-04-30 551
551








