Динамическая система

Динамическая система представляет математическую модель функционирования объекта анализа в пространстве и времени. Чтобы модель охватила широкий класс реальных объектов необходимо исходить из самых общих предположений о характере объекта. Поэтому система определяется в терминах наблюдаемых свойств и взаимосвязи между ними.

Под процессом функционирования понимается изменение состояния системы под действием внутренних и внешних причин. При этом состояние системы в фиксированный момент времени представляет вектор наблюденных значений переменных (проявлений свойств).

Определим динамическую систему в виде отношения на множествах X, Y, T, C.

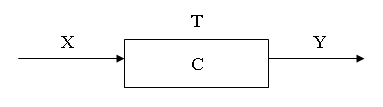
Множества X и Y представляет воздействия на систему внешней среды и ее реакции. Далее будем их называть входными и выходными переменными. Множество Т представляет множество [t₀, t₁, t₂,...] множеств времени в интервале наблюдения.

Z_i = <a₁, m₁, a₂, m₂,..., a_N, m_N>

Полное множество состояний системы образует фазовое пространство состояний динамической системы. Изменение состояния системы это переход из одной точки фазового пространства Cⁱ в другую C_j. Он происходит под воздействием входных сигналов X_k ⊂ X. Процесс переходов Cⁱ → C^j → C_c →... → C_p происходит во времени.

Рассмотрим процесс переходов системы в фазовом пространстве состояний.

Пусть в начальный момент наблюдения t₀ система находилась в некотором состоянии, который будем называть начальное состояние C_t0. Множество всех возможных начальных состояний есть декартовое произведение t₀ × C. Множество всех возможных входных сигналов в моменты времени t₁, t₂,... тоже есть декартово произведение Т × Х.

Множество всех возможных переходов системы в интервале наблюдения под воздействием входных сигналов представляет соотношение вида

(t₀ × C) × (T × X) × C

Процесс переходов системы в фазовом пространстве, наблюдаемый во времени, представляет собой множество отношений упорядоченности декартово произведение, что видно из рисунка.

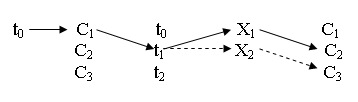
Математическая модель этого процесса имеет вид отображения

P: (t₀ × Z) × (t₁ × X) → Z_t1

В общем случае ее можно записать в следующем виде

Сt = P{(t₀,..., t), C_t0, X},

где Р — множество операторов перехода системы в фазовом пространстве состояний.

Выходная реакция системы в любой момент времени определяется состоянием системы в этот момент времени. Поэтому справедливо следующее соотношение.

Y_t = G{Z_t}.

где C_Z — множество оператор выходов.

Таким образом, динамическая система представляет собой множество

S = (P, G, X, Y, C, T).

Как следует из соотношений (и) это множество можно представить в виде декомпозиции

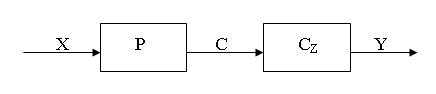
Наиболее общими свойствами динамических систем являются устойчивость и управляемость.