Задание 1. Найти производную скалярного поля u = u (x, y,z) в точке М 1 по направлению градиента скалярного поля v = v (x, y, z), вычисленного в точке М 2. Выяснить, возрастает или убывает скалярное поле в этой точке по данному направлению.
Задание приведено в таблице 1.
Таблица1 – Данные задания 1
| В-т | u = u (x, y, z) | М 1(x 1, y 1, z 1 ) | v = v (x, y, z) | М 2(x 2, y 2, z 2) |
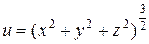
| (1, – 1, 0) | 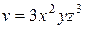
| (1, – 1, 1) | |
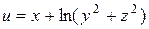
| (2; 1; 1) | 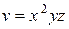
| (2, 1, 2) | |
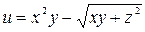
| (1, 5, – 2) | 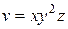
| (1, – 2, 1) | |
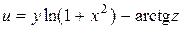
| (0, 1, 1) | 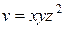
| (3, 2, 1) | |
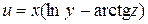
| (– 2, 1, – 1) | 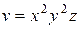
| (– 1, – 1, 3) | |
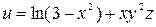
| (1, 3, 2) | 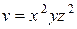
| (2, 1, – 1) | |
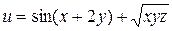
| (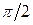 , , 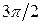 , 3) , 3)
| 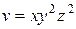
| (– 2, 1, 1) | |
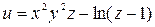
| (1, 1, 2) | 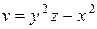
| (– 1, 1, 1) | |
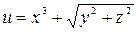
| (1, – 3, 4) | 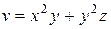
| (– 1, – 2, 1) | |
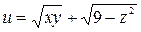
| (1, 1, 0) | 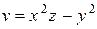
| (1, 1, – 2) | |
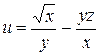
| (4, 1, – 2) | 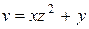
| (2, 2, 1) | |
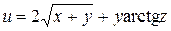
| (3, – 2, 1) | 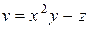
| (– 2, 2, 1) | |
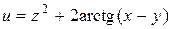
| (1, 2, – 1) | 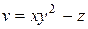
| (– 1, 2, 1) | |
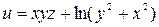
| (1, – 1, 2) | 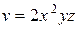
| (– 1, 1, 2) | |
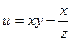
| (– 4, 3, – 1) | 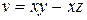
| (– 1, 2, 1) | |
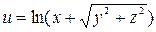
| (1, – 3, 4) | 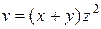
| (0, – 1, 2) | |
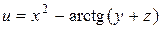
| (2, 1, 1) | 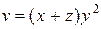
| (2, 2, 2) | |
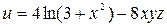
| (1, – 1, 0) | 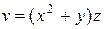
| (1, – 1, 1) |
Продолжение таблицы 1
| В-т | u = u (x, y, z) | М 1(x 1, y 1, z 1 ) | v = v (x, y, z) | М 2(x 2, y 2, z 2) |
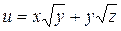
| (2, 4, 4) | 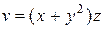
| (–1, – 1, – 1) | |
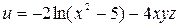
| (1, 1, 1) | 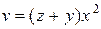
| (1, 1, – 1) | |
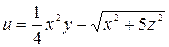
| (– 2, 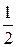 , 1) , 1)
| 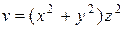
| (1, 1, 2) | |
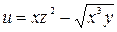
| (2, 2, 4) | 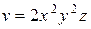
| (– 2, – 1, 1) | |
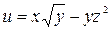
| (2, 1, – 1) | 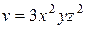
| (1, – 1, – 1) | |
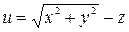
| (3, 4, 1) | 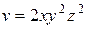
| (1, 1, – 1) | |
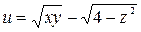
| (1, 1, 0) | 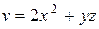
| (– 1, – 1, 2) |
Задание 2. Найти наибольшую плотность циркуляции векторного поля 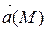 в точке М 0(х 0, у 0, z 0).
в точке М 0(х 0, у 0, z 0).
Задание приведено в таблице 2.
Таблица 2 – Данные задания 2
| В-т | В-т | ||
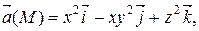 М 0(0, 1, – 2)
М 0(0, 1, – 2)
| 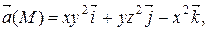 М 0(1, – 2, 0)
М 0(1, – 2, 0)
| ||
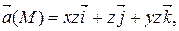 М 0(3, 0, 1)
М 0(3, 0, 1)
| 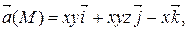 М 0(– 1, 0, 3)
М 0(– 1, 0, 3)
| ||
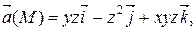 М 0(2, 1, – 1)
М 0(2, 1, – 1)
| 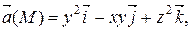 М 0(– 2, 1, 1)
М 0(– 2, 1, 1)
| ||
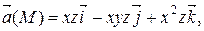 М 0(0, 1, 1)
М 0(0, 1, 1)
| 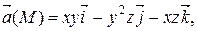 М 0(0, – 2, 1)
М 0(0, – 2, 1)
| ||
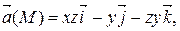 М 0(0, 1, 2)
М 0(0, 1, 2)
| 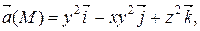 М 0(– 1, 2, 1)
М 0(– 1, 2, 1)
| ||
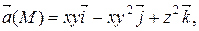 М 0(0, – 1, 1)
М 0(0, – 1, 1)
| 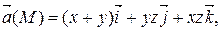 М 0(2, 1, 0)
М 0(2, 1, 0)
| ||
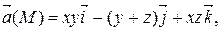 М 0(4, 0, 1)
М 0(4, 0, 1)
| 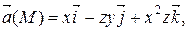 М 0(– 3, 0, 2)
М 0(– 3, 0, 2)
| ||
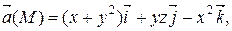 М 0(1, 0, 4)
М 0(1, 0, 4)
| 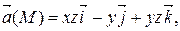 М 0(0, – 1, 4)
М 0(0, – 1, 4)
|
Продолжение таблицы 2
| В-т | В-т | ||
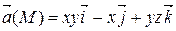 М 0(2, 2, 2)
М 0(2, 2, 2)
| 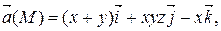 М 0(4, 1, – 3)
М 0(4, 1, – 3)
| ||
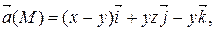 М 0(– 4, 1, 0)
М 0(– 4, 1, 0)
| 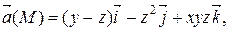 М 0(3, 0, 1)
М 0(3, 0, 1)
| ||
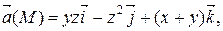 М 0(1, 3, 0)
М 0(1, 3, 0)
| 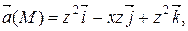 М 0(1, – 2, 1)
М 0(1, – 2, 1)
| ||
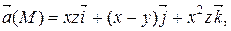 М 0(1, 1, – 2)
М 0(1, 1, – 2)
| 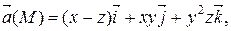 М 0(2, 2, 1)
М 0(2, 2, 1)
| ||
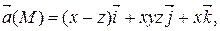 М 0(– 2, 2, 1)
М 0(– 2, 2, 1)
|
Задание 3. С помощью формулы Остроградского-Гаусса вычислить поток векторного поля 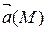 через внешнюю сторону поверхности пирамиды, ограниченной плоскостью (р) и координатными плоскостями х = 0, y = 0, z = 0.
через внешнюю сторону поверхности пирамиды, ограниченной плоскостью (р) и координатными плоскостями х = 0, y = 0, z = 0.
Задание приведено в таблице 3.
Таблица 3 – Данные задания 3
| В-т | 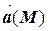
| (р) |
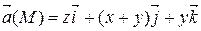
| 2 х + у + 2 z = 2 | |
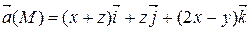
| 3 х + 2 у + z = 6 | |
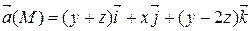
| 2 х + 2 у + z = 2 | |
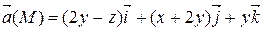
| х + 3 у + 2 z = 6 | |
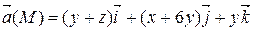
| х + 2 у + 2 z = 2 | |
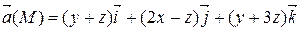
| 2 х + у + 3 z = 6 | |
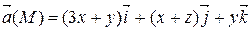
| х + 2 у + z = 2 | |
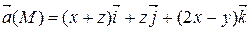
| 2 х + 2 у + z = 4 | |
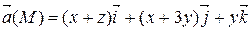
| х + у + 2 z = 2 | |
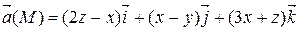
| х + у + 2 z = 2 |
Продолжение таблицы 3
| В-т | 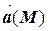
| (р) |
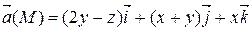
| х + 2 у + 2 z = 4 | |
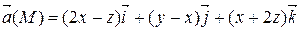
| х – у + z = 2 | |
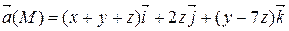
| 2 х + 3 у + z = 6 | |
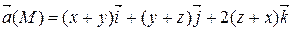
| 3 х – 2 у + 2 z = 6 | |
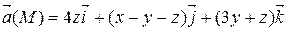
| х – 2 у + 2 z = 2 | |
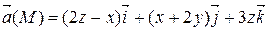
| х + 4 у + 2 z = 8 | |
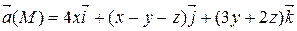
| 2 х + у + z = 4 | |
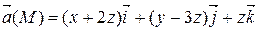
| 3 х + 2 у + 2 z = 6 | |
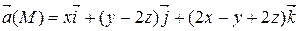
| х + 2 у + 2 z = 2 | |
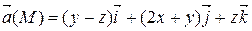
| 2 х + у + z = 2 | |
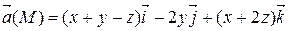
| х + 2 у + z = 2 | |
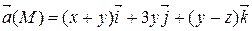
| 2 х – у – 2 z = –2 | |
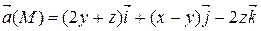
| х – у + z = 2 | |
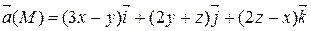
| 2 х – 3 у + z = 6 | |
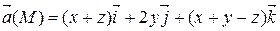
| х + 2 у + z = 2 |
Задание 4. Показать, что функция f (z) дифференцируемая всюду на комплексной плоскости и записать ее производную.
Задание приведено в таблице 4.
Таблица 4 – Функции f (z)
| В-т | f (z) | В-т | f (z) |
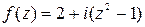
| 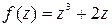
| ||
| f (z) = 3 + i (z 3 – 1) | f (z) = 3 i (z 2 + 2 z) | ||
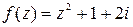
| 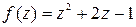
| ||
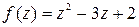
| 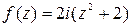
|
Продолжение таблицы 4
| В-т | f (z) | В-т | f (z) |
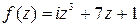
| 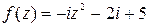
| ||
| f (z) = z 2 + z + 2 i | f (z) = 2 z 3 + 6 iz + i | ||
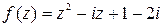
| 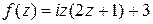
| ||
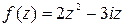
| 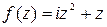
| ||
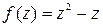
| 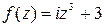
| ||
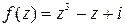
| 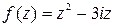
| ||
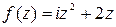
| 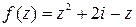
| ||
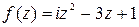
| f (z) = z 3 – iz + 2 | ||
| f (z) = iz (3 z – 5) + 2 |
Задание 5. Найти изображение F (p) по заданному оригиналу f (t).
Задание приведено в таблице 5.
Таблица 5 – Оригиналы f (t)
| В-т | f (t) | В-т | f (t) |
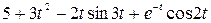
| 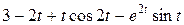
| ||
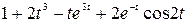
| 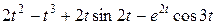
| ||
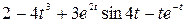
| 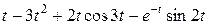
| ||
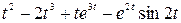
| 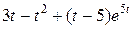
| ||
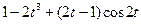
| 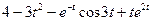
| ||
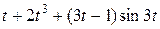
| 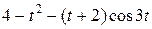
| ||
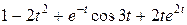
| 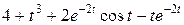
| ||
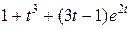
| 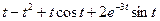
| ||
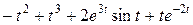
| 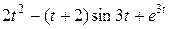
| ||
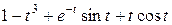
| 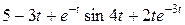
|
Продолжение таблицы 5
| В-т | f (t) | В-т | f (t) |
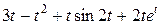
| 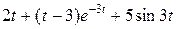
| ||
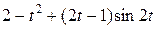
| 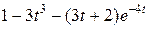
| ||
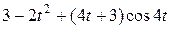
|
Задание 6. Операционным методом найти решение дифференциального уравнения, удовлетворяющего заданным начальным условиям.
Задание приведено в таблице 6.
Таблица 6 – Данные задания 6
| В-т | В-т | ||
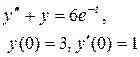
| 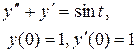
| ||
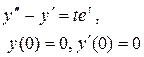
| 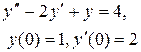
| ||
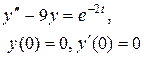
| 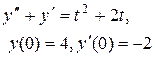
| ||
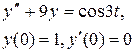
| 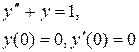
| ||
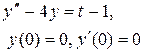
| 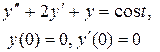
| ||
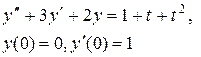
| 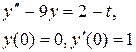
| ||
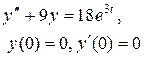
| 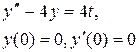
| ||
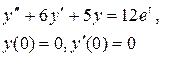
| 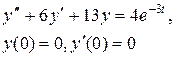
| ||
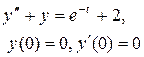
| 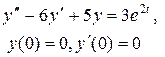
| ||
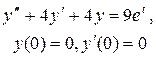
| 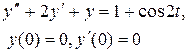
|
Продолжение таблицы 6
| В-т | В-т | ||
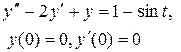
| 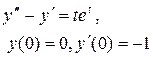
| ||
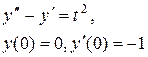
| 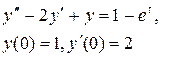
| ||
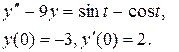
|
Задание 7. Методом Д’Aламбера найти уравнение u = u (x, t) формы однородной бесконечной струны, определяемой волновым уравнением
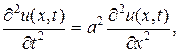
если в начальный момент t 0 = 0 форма струны и скорость точки струны с абсциссой х определяются соответственно заданными функциями (начальными условиями)
u(x, 0) = f (x),
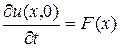 .
.
Задание приведено в таблице 7
Таблица 7 – Начальные условия
| В-т | В-т | ||
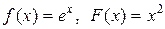
| 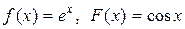
| ||
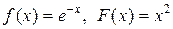
| 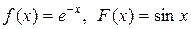
| ||
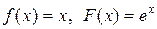
| 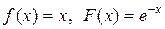
| ||
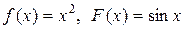
| 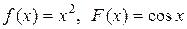
| ||
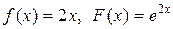
| 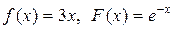
| ||
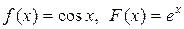
| 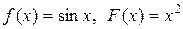
| ||
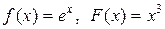
| 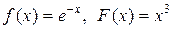
| ||
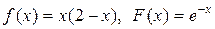
| 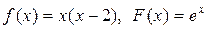
| ||
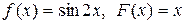
| 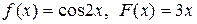
| ||
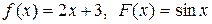
| 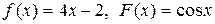
|
Продолжение таблицы 7
| В-т | В-т | ||
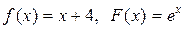
| 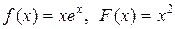
| ||
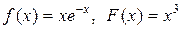
| 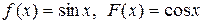
| ||
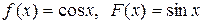
|
Задание 8. Решить задачу линейного программирования графическим методом:
max(min) Z = c 1 x 1 + c 2 x 2,
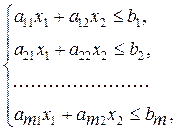
x 1 ≥ 0, x 2 ≥ 0.
Задание приведено в таблице8.
Таблица 8 – Данные задания 8
| В-т | В-т | В-т | |||
Z = 2 x 1 + x 2,
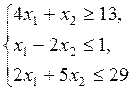 
| Z = x 1 + 5 x 2,
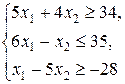 
| Z = x 1 + 5 x 2,
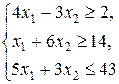
| |||
Z = 2 x 1 + 3 x 2,
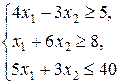
| Z = 4 x 1 + 3 x 2,
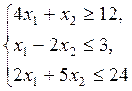
| Z = 5 x 1 + x 2,
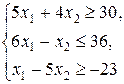
| |||
Z = 4 x 1 + x 2,
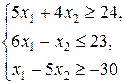
| Z = x 1 + 4 x 2,
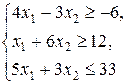
| Z = x 1 + x 2,
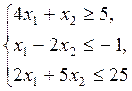
|
Продолжение таблицы 8
| В-т | В-т | В-т | |||
Z = 2 x 1 + 3 x 2,
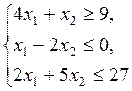 
| Z = 2 x 1 + 3 x 2,
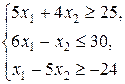 
| Z = x 1 + 2 x 2,
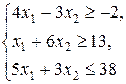 
| |||
Z = 2 x 1 + 3 x 2,
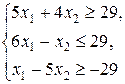
| Z = 3 x 1 + x 2,
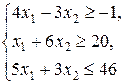
| Z = 2 x 1 + x 2,
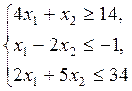
| |||
Z = 3 x 1 + x 2,
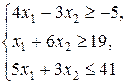
| Z = 3 x 1 + 2 x 2,
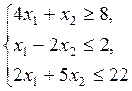
| Z = 2 x 1 + 3 x 2,
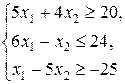
| |||
Z = x 1 + 2 x 2,
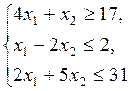
| Z = 3 x 1 + 4 x 2,
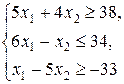
| Z = 3 x 1 + 2 x 2,
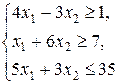
| |||
Z = 2 x 1 + x 2,
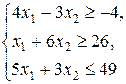
| Z = 2 x 1 + x 2,
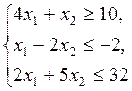
| Z = 3 x 1 + x 2,
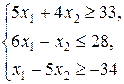
| |||
Z = x 1 + 2 x 2,
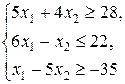
|
 2015-04-20
2015-04-20 436
436








