Рассмотрим линейное дифференциальное уравнение второго порядка с постоянными коэффициентами
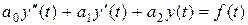 , (1)
, (1)
f (t) – непрерывная функция действительного переменного.
Требуется найти частное решение уравнения, удовлетворяющее начальным условиям:
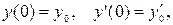 (2)
(2)
где 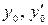 – заданные числа (задача Коши).
– заданные числа (задача Коши).
Будем предполагать, что функция f (t) является оригиналом. Искомую функцию y (t) и её производные 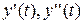 также предполагаем оригиналами. Полагаем f (t)
также предполагаем оригиналами. Полагаем f (t) 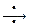 F (p), y (t)
F (p), y (t) 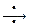 Y (p).
Y (p).
Для решения поставленной задачи (1), (2) перейдём от уравнения (1) к изображающему (или операторному) уравнению, связывающему изображения Y (p) и F (p).
Применяя два раза теорему о дифференцировании оригинала, получим:
у ′(t) 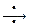 pY (p) – y 0,
pY (p) – y 0,
y ″(t) 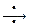 p 2 Y (p) – py 0 – у 0′
p 2 Y (p) – py 0 – у 0′
Далее, применяя теорему линейности, перейдём от уравнения (1) к операторному уравнению:
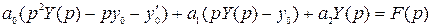 . (3)
. (3)
Из уравнения (3) выразим 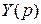 .Искомое частное решение y (t) является оригиналом, соответствующим данному изображению. Оно определяется с помощью таблиц соответствия.
.Искомое частное решение y (t) является оригиналом, соответствующим данному изображению. Оно определяется с помощью таблиц соответствия.
Пример 2. Найти частное решение уравнения 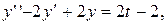 удовлетворяющее начальным условиям:
удовлетворяющее начальным условиям: 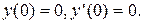
Решение. Обозначим через y (t) искомое частное решение, через Y (p) – его изображение. Тогда
у ′ 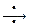 pY (p) – y (0) = pY (p),
pY (p) – y (0) = pY (p),
y ″ 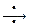 p 2 Y (p) – py (0) – у ′(0) = p 2 Y (p),
p 2 Y (p) – py (0) – у ′(0) = p 2 Y (p),
2 t – 2 
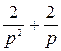 =
= 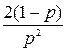 .
.
Операторное уравнение будет иметь вид
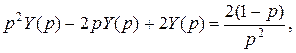
откуда
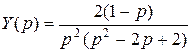 .
.
Дробь 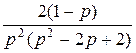 представим в виде суммы простых дробей и найдем коэффициенты этого представления:
представим в виде суммы простых дробей и найдем коэффициенты этого представления:
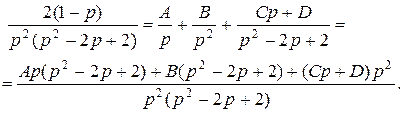
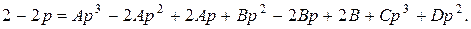
Из системы:
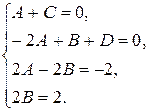
Откуда 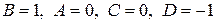 .
.
Тогда
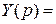
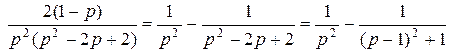 .
.
Используя таблицы соответствия, найдём: Y (p) 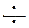 t – et sin t.
t – et sin t.
Таким образом, искомое частное решение
y (t) = t – et sin t.
Ответ: y (t) = t – et sin t.
Задание 7. Рассмотрим задачу Коши для бесконечной однородной струны. Пусть требуется найти решение волнового уравнения
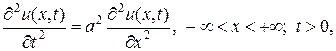
при начальных условиях
u (x, 0) = f (x),
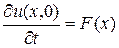 .
.
Искомое решение задачи Коши для бесконечной струны u (x, t) определяется по формуле
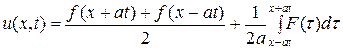 ,
,
которая называется формулой Д’Aламбера или решением Д’Aламбера.
Пример. Методом Д’Aламбера найти уравнение u = u (x, t) формы однородной бесконечной струны, определяемой волновым уравнением
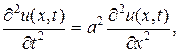
если в начальный момент t 0 = 0 форма струны и скорость точки струны с абсциссой х определяются соответственно заданными функциями
u(x, 0) = f (x), 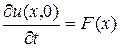 .
.
Здесь начальная форма струны f (x) = ex, а начальная скорость ее F (x) = cos2 x.
Решение. Искомое решение u (x, t) найдем по формуле Д’Aламбера:
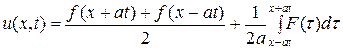 .
.
Так как f (x) = ex, F (x) = cos2 x, то
и (х, t) = 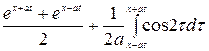 =
= 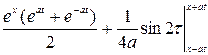 =
=
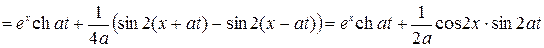 .
.
Ответ: и (х, t) = 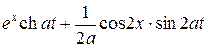 .
.
Задание 8. Рассмотрим задачу линейного программирования:
max(min) Z = c 1 x 1 + c 2 x 2,
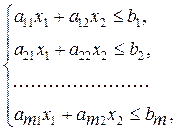
x 1 ≥ 0, x 2 ≥ 0.
Строим область допустимых решений Ω, которая является пересечением полуплоскостей, определяемых неравенствами системы ограничений вида ai 1 x 1 + ai 2 x 2 ≤ bi, i = 1, …, m. Известно, что прямая ai 1 x 1 + ai 2 x 2 = bi делит плоскость на две полуплоскости, причем для любой точки (x 1; x 2) одной полуплоскости ai 1 x 1 + ai 2 x 2 ≤ bi, а для любой точки (x 1; x 2) другой полуплоскости ai 1 x 1 + ai 2 x 2 ≥ bi. Другими словами, решением неравенства
ai 1 x 1 + ai 2 x 2 ≤ bi
является одна из полуплоскостей, ограниченная прямой ai 1 x 1 + ai 2 x 2 = bi (и является выпуклым множеством).
Чтобы уточнить, какая полуплоскость является решением конкретного неравенства, достаточно подставить в него координаты любой точки одной полуплоскости: если числовое неравенство верно, то эта полуплоскость является решением неравенства, если нет – то другая. На практике удобно в качестве такой точки выбирать начало координат х = 0, у = 0. Искомая область Ω является пересечением построенных выпуклых множеств и также является выпуклым множеством.
Вектор 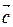 = (с 1; с 2), где с 1 =
= (с 1; с 2), где с 1 = 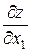 , с 2 =
, с 2 = 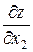 , называется вектором градиентом целевой функции Z = Z (х 1; х 2). Он показывает направление наискорейшего возрастания функции. Вектор –
, называется вектором градиентом целевой функции Z = Z (х 1; х 2). Он показывает направление наискорейшего возрастания функции. Вектор – 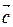 (антиградиент) показывает направление наискорейшего убывания функции.
(антиградиент) показывает направление наискорейшего убывания функции.
Вектор 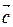 = (с 1; с 2) перпендикулярен к прямым Z = const, которые называются линиями уровня целевой функции.
= (с 1; с 2) перпендикулярен к прямым Z = const, которые называются линиями уровня целевой функции.
Порядок графического решения задачи линейного программирования (ЗЛП):
1) с учетом условий ограничений строим область допустимых решений Ω;
2) строим вектор 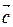 = (с 1; с 2) наискорейшего возрастания целевой функции;
= (с 1; с 2) наискорейшего возрастания целевой функции;
3) проводим произвольную линию Z = Z 0 (проще провести линию нулевого уровня Z = 0) перпендикулярно вектору 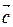 ;
;
4) при нахождении max Z (х 1; х 2) перемещаем линию уровня Z = Z 0 в направлении вектора 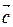 так, чтобы она касалась области Ω в ее крайнем положении (крайней точке). При нахождении min Z (х 1; х 2) поступаем аналогично, перемещая линию уровня в антиградиентном направлении;
так, чтобы она касалась области Ω в ее крайнем положении (крайней точке). При нахождении min Z (х 1; х 2) поступаем аналогично, перемещая линию уровня в антиградиентном направлении;
5) определяем оптимальные планы
Х 1* = (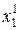 *,
*, 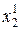 *) и Х 2* = (
*) и Х 2* = (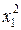 *,
*, 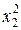 *)
*)
и экстремальные значения целевой функции
Z min = Z (Х 1*) и Z max = Z (Х 2*).
Пример. Решить задачу линейного программирования графическим методом:
max(min) Z = 3 x 1 + 2 x 2,
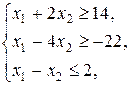
x 1 ≥ 0, x 2 ≥ 0.
Решение. Построим область допустимых решений Ω. Из теории следует, что это будет выпуклое множество. Для этого запишем уравнения границ области допустимых решений. Заменив в ограничениях знак неравенства знаком равенства
x 1 + 2 x 2, = 14, (I)
x 1 – 4 x 2, = – 22, (II)
x 1 – x 2, = 2, (III)
построим эти прямые.
Определим полуплоскости, удовлетворяющие неравенствам ограничениям. Пересечение этих полуплоскостей образует треугольник АВС, который и является областью допустимых решений Ω. Покажем ее на рисунке 2 штриховкой.
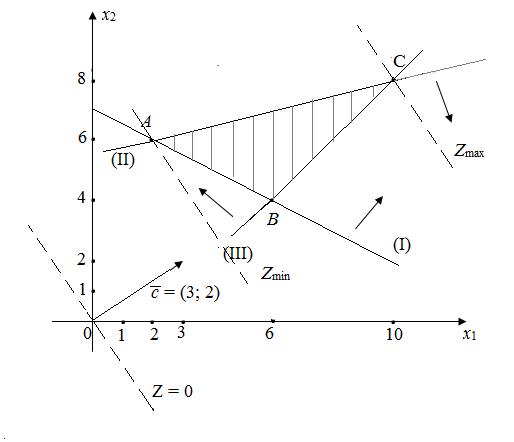
Рисунок 2 – Область допустимых решений Ω
Строим вектор 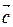 = (3; 2) – градиент целевой функции Z (х 1; х 2).
= (3; 2) – градиент целевой функции Z (х 1; х 2).
Далее проводим линию нулевого уровня 3 x 1 + 2 x 2, = 0, перпендикулярную вектору 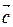 = (3; 2).
= (3; 2).
Перемещаем линию нулевого уровня в направлении вектора 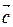 . Первой точкой контакта линии уровня с треугольником АВС является точка А и, следовательно, Z min = Z (А). Последняя точка контакта – точка С, и следовательно, Z max = Z (C).
. Первой точкой контакта линии уровня с треугольником АВС является точка А и, следовательно, Z min = Z (А). Последняя точка контакта – точка С, и следовательно, Z max = Z (C).
Найдем координаты точек A и С и вычислим экстремальные значения целевой функции.
Точка A – точка пересечения прямых (I) и (II).
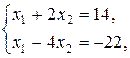
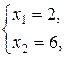
А (2; 6), Z min = Z (А) = Z (2; 6) = 3·2 + 2·6 = 18.
Точка С – точка пересечения прямых (II) и (III).
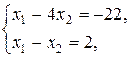
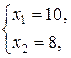
С (10; 8), Z max = Z (C) = Z (10; 8) = 3·10 + 2·8 = 46.
Ответ: Z min = 18, Z max = 46.
Вопросы для подготовки к зачету
 2015-04-20
2015-04-20 869
869








