Задание 1. Стационарным скалярным полем называется пространство R n (или его часть – область V), в каждой точке М которого определенна скалярная функция (числовая функция) u (M). В частности, в трехмерном пространстве математически скалярное поле может быть определено в данной области V заданием скалярной функции
u = u (M) = u (x, y, z).
Эту функцию, независимо от ее физического смысла, называют потенциалом скалярного поля.
При изучении скалярного поля важно знать скорость изменения функции u (x, y, z), задающей это поле, при переходе от одной точки поля к другой.
Производной функции u = u (x, y, z) в точке М 0(х 0, у 0, z 0) по направлению вектора 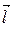 называется предел (если он существует) отношения приращения функции Δ u к величине перемещения
называется предел (если он существует) отношения приращения функции Δ u к величине перемещения 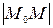 , когда последнее стремится к нулю:
, когда последнее стремится к нулю:
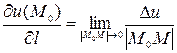
или
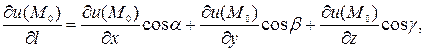

где 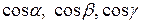 – направляющие косинусы вектора
– направляющие косинусы вектора 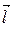 .
.
Вектор, координатами которого являются значения частных производных функции u (x, y, z) в точке M 0(x 0, y 0, z 0), называется градиентом скалярного поля в точке М 0
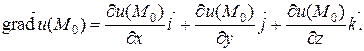
Пример. Найти производную скалярного поля 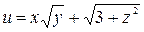 в точке М 1(2, 1, 1) по направлению градиента скалярного поля
в точке М 1(2, 1, 1) по направлению градиента скалярного поля 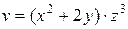 , вычисленного в точке М 2(1, – 1, 1). Выяснить, возрастает или убывает скалярное поле в этой точке по данному направлению.
, вычисленного в точке М 2(1, – 1, 1). Выяснить, возрастает или убывает скалярное поле в этой точке по данному направлению.
Решение. Найдем градиент векторного поля 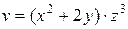 в точке М 2(1, – 1, 1). По определению
в точке М 2(1, – 1, 1). По определению
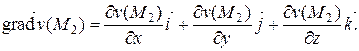
Найдем частные производные функции v (x, y, z):
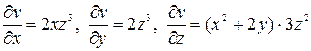
и вычислим их значения в точке М 2(1, – 1, 1):

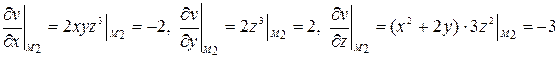 .
.
Следовательно,
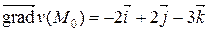 ,
, 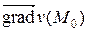 = (– 2, 2, –3).
= (– 2, 2, –3).
Далее, найдем производную скалярного поля 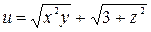 в точке М 1(2, 1, 1) по направлению
в точке М 1(2, 1, 1) по направлению 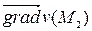 по формуле
по формуле
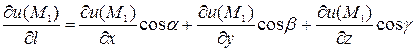 .
.
Для этого найдем частные производные функции u (x, y, z):
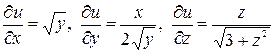 .
.
и вычислим их значения в точке М 1(2, 1, 1):
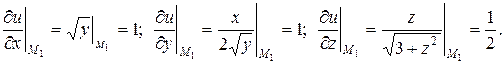
Так как
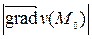 =
= 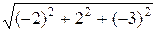 =
= 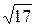 ,
,
то его направляющие косинусы равны:
cosα = 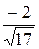 , cosβ =
, cosβ = 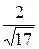 , cosγ =
, cosγ = 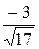 .
.
Следовательно,
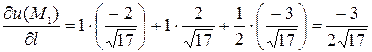 .
.
Поскольку 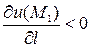 , то заданная функция в направлении
, то заданная функция в направлении  убывает.
убывает.
Ответ: 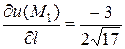 . Функция в направлении
. Функция в направлении 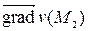 убывает.
убывает.
Задания 2, 3. Стационарным векторным полем называется пространство R n (или его часть – область V), в каждой точке М которого определена векторная функция  =
=  . В пространстве R3 в случае декартовой системы координат векторное поле записывается в виде
. В пространстве R3 в случае декартовой системы координат векторное поле записывается в виде
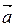 =
= 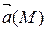 = P (x, y, z)
= P (x, y, z) 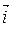 + Q (x, y, z)
+ Q (x, y, z) 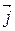 + R (x, y, z)
+ R (x, y, z) 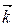
и определяется тремя скалярными функциями P (x, y, z), Q (x, y, z), R (x, y, z) – проекциями вектора 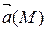 на координатные оси.
на координатные оси.
Пусть в области V 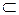 R3 задано векторное поле
R3 задано векторное поле 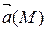 = (P, Q, R) и функции P (x, y, z), Q (x, y, z), R (x, y, z) имеют частные производные в точке M (x, y, z)
= (P, Q, R) и функции P (x, y, z), Q (x, y, z), R (x, y, z) имеют частные производные в точке M (x, y, z) 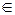 V по х, у, z соответственно. Тогда дивергенция или расходимость векторного поля
V по х, у, z соответственно. Тогда дивергенция или расходимость векторного поля 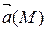 в точке М,обозначаемая
в точке М,обозначаемая 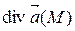 , определяется по формуле
, определяется по формуле
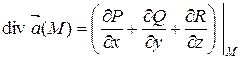 .
.
С физической точки зрения 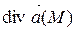 характеризует мощность находящегося в точке М источника или стока векторного поля
характеризует мощность находящегося в точке М источника или стока векторного поля 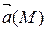 , то есть мощность находящегося в точке М источника, если
, то есть мощность находящегося в точке М источника, если 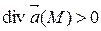 и стока, если
и стока, если 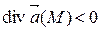 . В случае, когда
. В случае, когда 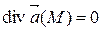 , в точке М нет ни источника, ни стока.
, в точке М нет ни источника, ни стока.
Ротор или вихрь векторного поля 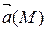 = (P, Q, R) это вектор, который обозначается
= (P, Q, R) это вектор, который обозначается 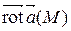 и вычисляется следующим образом:
и вычисляется следующим образом:

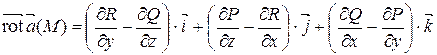 .
.
Для удобства запоминания ротора его можно записать с помощью символьного определителя:
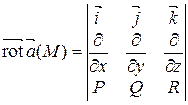 .
.
Линия L называется ориентированной, если на ней выбрано направление перемещения. Для гладкой линии L в качестве ориентирующего вектора может быть выбран единичный вектор 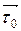 , направленный в каждой ее точке по касательной к ней в сторону перемещения. Линия называется гладкой, если в каждой ее точке существует касательная. Если уравнение линии y = f (x), то гладкость означает, что функция y = f (x) – дифференцируемая.
, направленный в каждой ее точке по касательной к ней в сторону перемещения. Линия называется гладкой, если в каждой ее точке существует касательная. Если уравнение линии y = f (x), то гладкость означает, что функция y = f (x) – дифференцируемая.
Если задано векторное поле 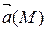 = (P, Q, R) и некоторая замкнутая, ориентированная (кусочно-гладкая) кривая L в пространстве R 3, то криволинейный интеграл
= (P, Q, R) и некоторая замкнутая, ориентированная (кусочно-гладкая) кривая L в пространстве R 3, то криволинейный интеграл
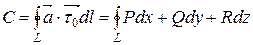
называется циркуляцией векторного поля 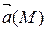 вдоль контура L,где
вдоль контура L,где 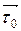 – единичный вектор, направленный по касательной к кривой L и указывающий направление обхода по контуру.
– единичный вектор, направленный по касательной к кривой L и указывающий направление обхода по контуру.
Число
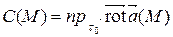
называется плотностью циркуляции векторного поля 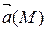 в точке М в направлении вектора
в точке М в направлении вектора 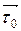 . Вектор
. Вектор 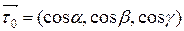 – единичный вектор касательной. Плотность достигает максимума в направлении
– единичный вектор касательной. Плотность достигает максимума в направлении 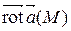 и равна
и равна 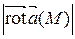 , т.е.
, т.е. 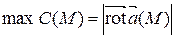 .
.
Поток П векторного поля 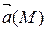 , через ориентированную поверхность S равен значению интеграла по поверхности от скалярного произведения вектора поля на единичный вектор
, через ориентированную поверхность S равен значению интеграла по поверхности от скалярного произведения вектора поля на единичный вектор 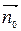 нормали к поверхности. Для потока векторного поля принято представление:
нормали к поверхности. Для потока векторного поля принято представление:
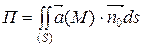 .
.
Пусть S – замкнутая кусочно–гладкая поверхность, единичный вектор внешней нормали к которой 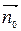 . Тогда поток П вектора
. Тогда поток П вектора 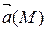 = (P, Q, R) через замкнутую ориентированную в направлении внешней нормали поверхность S можно вычислить с помощью формулы Остроградского–Гаусса:
= (P, Q, R) через замкнутую ориентированную в направлении внешней нормали поверхность S можно вычислить с помощью формулы Остроградского–Гаусса:
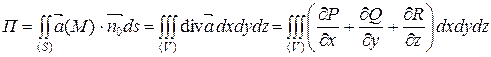 .
.
Пример 1. Найти наибольшую плотность циркуляции векторного поля 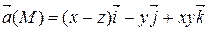 в точке М 0(1, – 1, 0).
в точке М 0(1, – 1, 0).
Решение. Наибольшая плотность циркуляции векторного поля 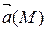 в данной точке М 0 достигается в направлении ротора поля и численно равна
в данной точке М 0 достигается в направлении ротора поля и численно равна 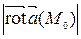 . Найдем:
. Найдем:
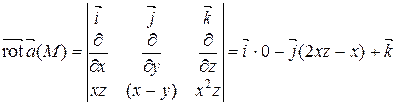 ,
,
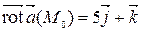 . Тогда
. Тогда
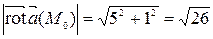 .
.
Ответ: 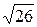 .
.
Пример 2. С помощью формулы Остроградского – Гаусса вычислить поток векторного поля
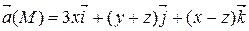
через внешнюю сторону поверхности пирамиды, ограниченной плоскостью (р): х + 3 у + z = 3 и координатными плоскостями х = 0, y = 0, z = 0.
Решение. Заданная векторная функция определена и дифференцируема в каждой точке области (V), ограниченной поверхностью пирамиды (рисунок 1).
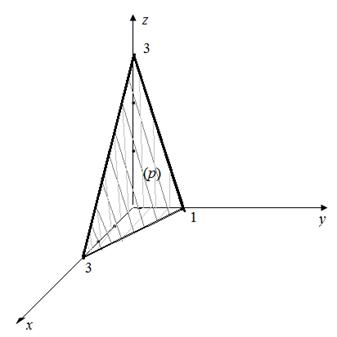
Рисунок 1 – Чертеж области V
Тогда поток векторного поля 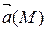 в заданном направлении можно вычислить по формуле Остроградского – Гаусса:
в заданном направлении можно вычислить по формуле Остроградского – Гаусса:
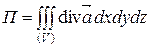 .
.
Найдем дивергенцию векторного поля 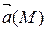 :
:
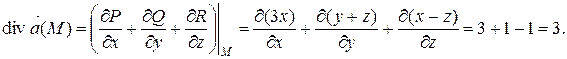 Тогда
Тогда
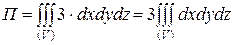 .
.
Вычислим тройной интеграл по области V, получим:
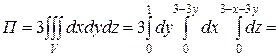
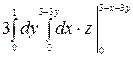 =
= 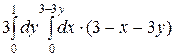 =
=
= 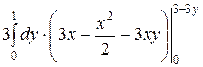 =
= 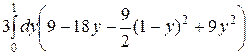 =
=
= 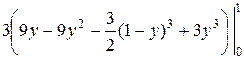
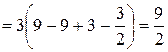 .
.
Ответ: П = 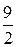 .
.
Задание 4. Пусть однозначная функция 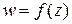 определена в некоторой области G комплексной плоскости z и точки z и z + ∆ z принадлежат области G. Приращение функции w в точке z имеет вид:
определена в некоторой области G комплексной плоскости z и точки z и z + ∆ z принадлежат области G. Приращение функции w в точке z имеет вид:
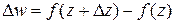 , где
, где 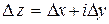 .
.
Производной 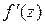
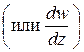 функции
функции 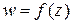 в точке
в точке 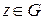 называется предел отношения
называется предел отношения 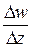 при
при 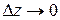 по любому закону, если он существует, т.е.
по любому закону, если он существует, т.е.
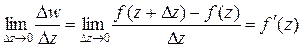 .
.
Если в точке z существует производная 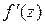 , то функция
, то функция 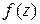 называется дифференцируемой в точке z.
называется дифференцируемой в точке z.
Для того чтобы функция 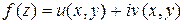 была дифференцируемой в точке
была дифференцируемой в точке 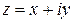 , необходимо и достаточно, чтобы функции u (x, y) и v (x, y) были дифференцируемы в точке (x, y) как функции двух действительных переменных и выполнялись соотношения:
, необходимо и достаточно, чтобы функции u (x, y) и v (x, y) были дифференцируемы в точке (x, y) как функции двух действительных переменных и выполнялись соотношения:
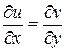 ,
, 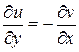 .
.
Эти соотношения называются условиями Коши-Римана.
Производную можно найти по одной из формул:
f ′(z) = 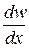 =
= 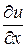 + i
+ i 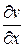 ; f ′(z) =
; f ′(z) = 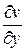 – i
– i 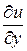 ;
;
f ′(z) = 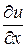 – i
– i 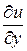 ; f ′(z) =
; f ′(z) = 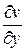 + i
+ i 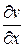 .
.
Пример. Показать, что функция f (z) = iz 3 + z 2 – 3 iz дифференцируемая всюду на комплексной плоскости и записать ее производную.
Решение. Определим действительную и мнимую части функции f (z) = iz 3 + z 2 – 3 iz, т.е. представим функцию 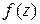 в виде
в виде
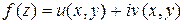 .
.
Так как 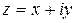 , то
, то
f (z) = iz 3 + z 2 – 3 iz = i (x + iy)3 + (x + iy)2 – 3 i (x + iy) =
= i (x 3 + 3 x 2 yi – 3 xy 2 – y 3 i) + x 2 + 2 xyi – y 2 – 3 x i + 3 y =
= x 3 i – 3 x 2 y – 3 xy 2 i + y 3 + x 2 + 2 xyi – y 2 – 3 xi + 3 y =
= (y3 + x 2 – y 2 – 3 x 2 y + 3 y) + i (x 3 – 3 xy 2 + 2 xy – 3 x).
Следовательно,
u (x, y) = y3 + x 2 – y 2 – 3 x 2 y + 3 y,
v (x, y) = x 3 – 3 xy 2 + 2 xy – 3 x.
Проверим выполнение условий Коши–Римана:
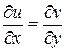 ,
, 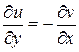 .
.
Найдем частные производные функций u (x, y) и v (x, y):
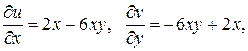
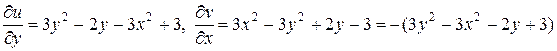 .
.
Условия Коши-Римана выполняются при всех значениях х и у, следовательно, функция f (z) = iz 3 + z 2 – 3 iz является дифференцируемой на всей комплексной плоскости. При этом
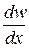 = 2 х – 6 ху – i (3 y 2 – 2 y –3 x 2 – 3).
= 2 х – 6 ху – i (3 y 2 – 2 y –3 x 2 – 3).
Ответ: 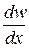 = 2 х – 6 ху – i (3 y 2 – 2 y –3 x 2 – 3).
= 2 х – 6 ху – i (3 y 2 – 2 y –3 x 2 – 3).
Задания 5,6. Любая комплексная функция f (t) действительного переменного t называется оригиналом, если она удовлетворяет следующим условиям:
1) f (t) – кусочно–непрерывная при t ≥ 0, это значит, что она либо непрерывна, либо в каждом конечном интервале имеет лишь конечное число точек разрыва 1-го рода;
2) f (t) ≡ 0 при t < 0;
3) при t → ∞ функция f (t) растёт не быстрее некоторой показательной функции (имеет ограниченную степень роста), т.е. существует такое положительное число М и такое неотрицательное число s, что для всех t ≥ 0 выполняется неравенство
| f (t) | ≤ M ∙ est, М > 0, s ≥ 0.
Точная нижняя грань s 0≥0 тех значений s, для которых выполняется указанное условие 3, называется показателем ро ста функции f (t).
Изображением функции f (t) по Лапласу (преобразованием Лапласа) называется функция F (p) комплексного переменного p = s + i  из некоторой области D комплексной плоскости p, определяемая равенством
из некоторой области D комплексной плоскости p, определяемая равенством
F (p) = 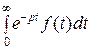 .
.
Связь между функциями f (t)и F (p) будем обозначать в дальнейшем следующим образом: f (t) 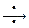 F (p) или F (p)
F (p) или F (p) 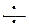 f (t).
f (t).
Первую запись следует читать так: «Оригинал f (t) имеет изображение F (p)». Вторую запись следует читать так: «Изображение F (p) имеет оригинал f (t)» или «f (t) является оригиналом изображения F (p)». Используются также и другие обозначения.
 2015-04-20
2015-04-20 9063
9063