Нахождение наибольшего и наименьшего значения функции на отрезке

Задача. Найти наибольшее и наименьшее значения функции:

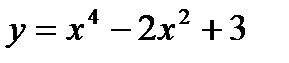на сегменте [-2; 2]

Решение: Найдём критические точки и исследуем их на экстремум.

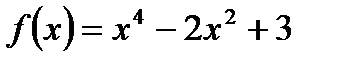
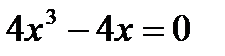
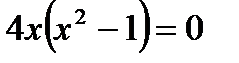
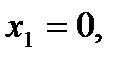
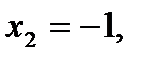
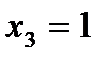
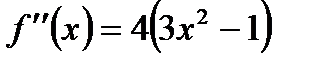
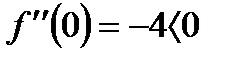
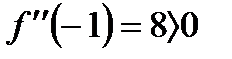
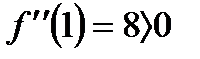
В точке x=0 функция имеет максимум, равный f(0)=3.

В каждой из точек x=-1 и x=1 функция имеет минимум, равный f (-1)=f (1)=2

Найдём значения функции на концах сегмента:

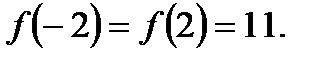
Итак, наибольшее значение равно 11, а наименьшее 2.

Задача. Найти радиус кривизны и координаты центра кривизны кривой 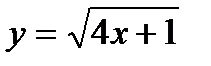в точке А (0; 1).

Решение: Радиус кривизны вычисляется по фор­муле:

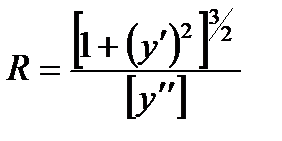
Дважды дифференцируя данную функцию, находим

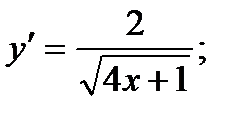
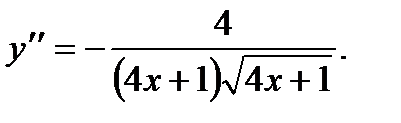
Вычислим значения производных у' и у" в заданной точке А (0; 1), т.е. при x = 0; имеем y¢(0) = 2; y¢¢ (0) = - 4.

Тогда радиус кривизны:

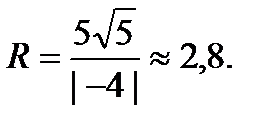
Для нахождения координат центра кривизны С(x_с; y_с] воспользуемся формулами:

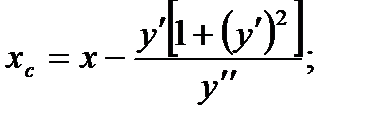
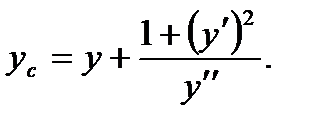
Подставив в эти формулы координаты точки А и найден­ные значения производных, получим:

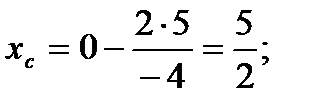
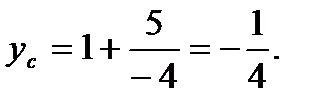
Итак, точка С (5/2; -1/4) — центр кривизны.

Кривая 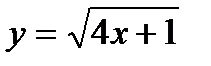, точка А (0; 1), центр кривизны С (5/2; -1/4) и радиус кривизны R»2,8.

Задача. Найти радиус кривизны кривой r = a sin3 j (трех лепестковая роза) в точке A (p/6; а).

Решение. Если кривая задана в полярной системе координат уравнением r=f (j), то ра­диус кривизны вычисляется по фор­муле: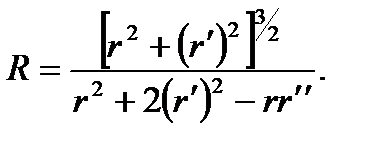

Дважды дифференцируя данную функ­цию r = a sin 3j, найдем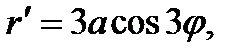

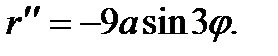
Вычислим значения производных r¢ и r¢¢ в точке A (p/6;a), т.е при j=p/6 и r =a.

Имеем: r¢ (p/6)=0 и r¢¢ (p/6)=-9a. Подставив в формулу r =a, r¢=0 и r¢¢=9a, получим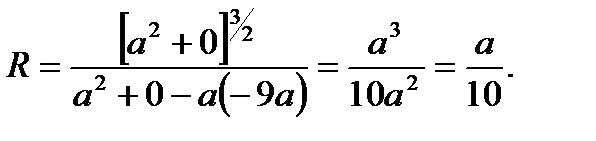

Вопросы для самопроверки.

1. Сформулируйте признаки возрастания (убывания) функции. Приведите примеры.

2. Дайте определение экстремума функции.

3. Как найти максимум, минимум функции (два правила)?

4. Приведите пример, когда обращение производной в нуль не является достаточным условием экстремума функции.

5. Как найти интервалы выпуклости (вогнутости) функции? Примеры.