Свойства дифференциалов

1. 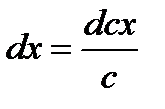, с- const

2. 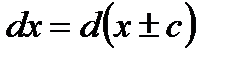Например: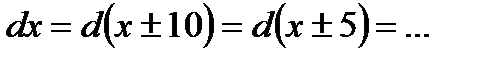

Под непосредственным интегрированием понимается сведение подынтегрального выражения к табличному виду путём использования тождественных преобразований, таблицы и свойств неопределённых интегралов и дифференциалов.

Например: Найти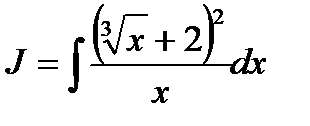

Решение: Возведём двучлен во вторую степень и запишем каждое слагаемое в виде степени, затем, произведя почленное деление и, применив соответствующие формулы таблицы, получим:

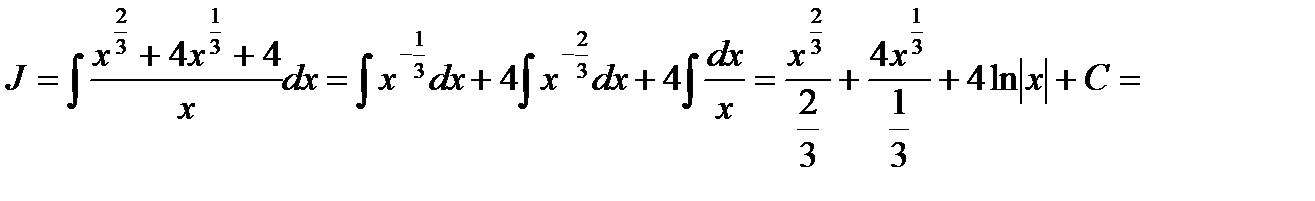
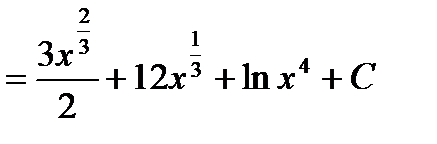
7.2 Способы интегрирования.

1. Подведение под знак дифференциала:

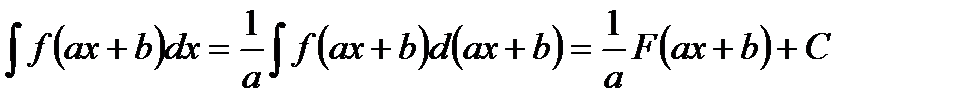
1. Интегрирование по частям:

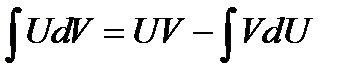
Классы функций, интегрируемых по частям:

a).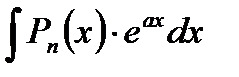

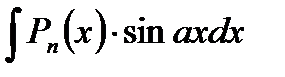
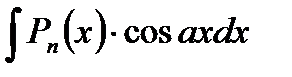
б).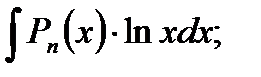

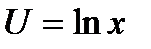
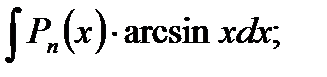
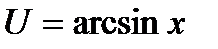
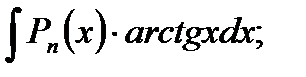
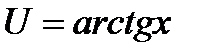
в).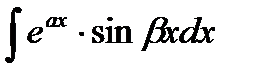

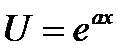
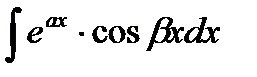или 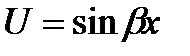или U= cosbx

3. Разложение правильной рациональной дроби на простейшие:

4. Интегралы вида

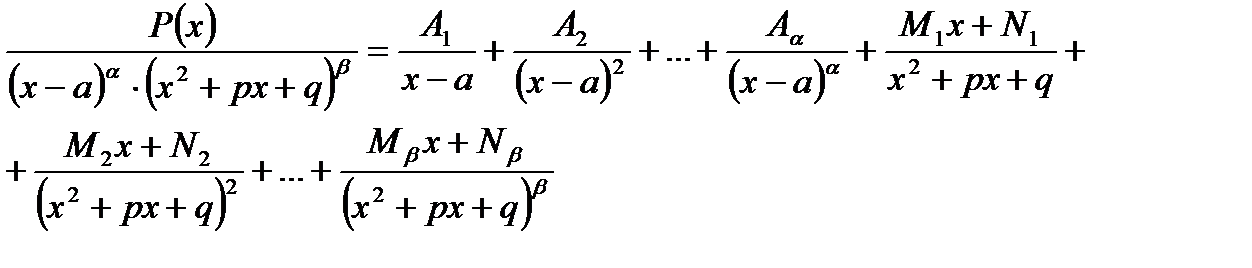
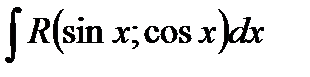
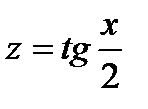-универсальная подстановка;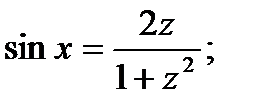

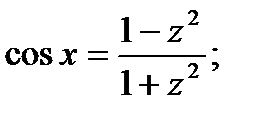
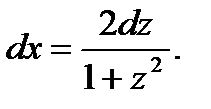
Для частных случаев:

а) формулы понижения порядка:

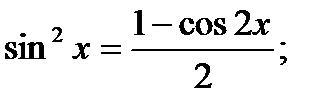
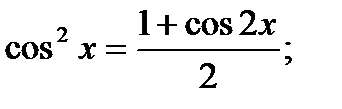
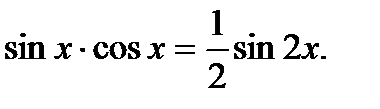
б) Формулы преобразования произведения тригонометрических функций в сумму:

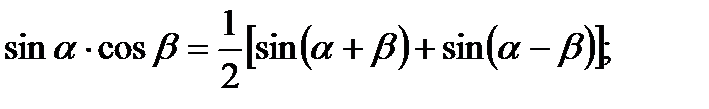
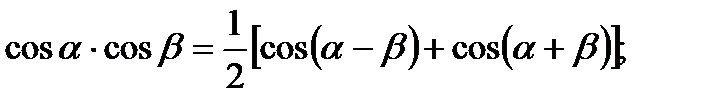
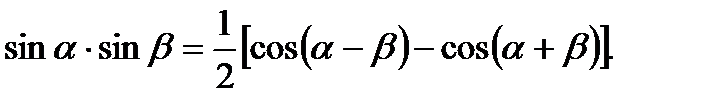
5. Интегралы вида 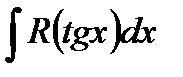и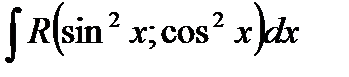

Подстановка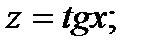

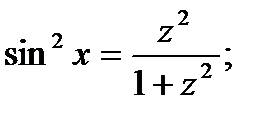
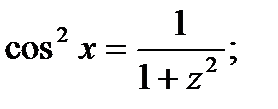
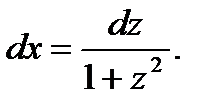
В частности:

для 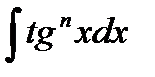применяется формула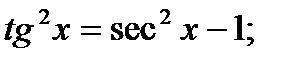

для 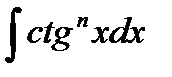-формула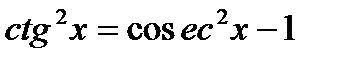

6. Интегрирование иррациональностей.

а) 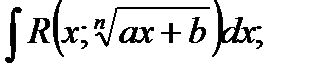подстановка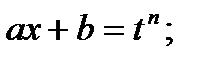

б) 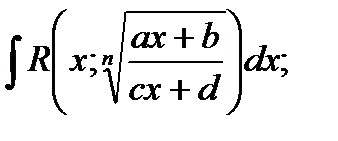подстановка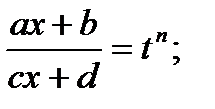

в) Тригонометрические подстановки:

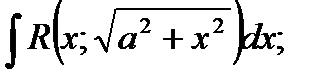
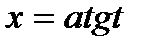
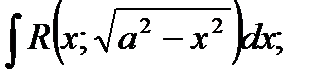
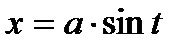
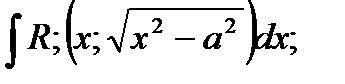
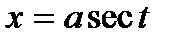
Например:

1) 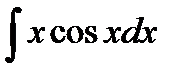решается способом интегрирования по частям.

2) 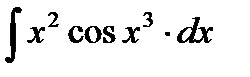решается способом подведения функции под знак дифференциала.

3) 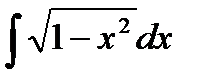- решается методом подстановки x=sint.

Примеры 1-3 решить самостоятельно.