1. Определение. Производной первого порядка от функции 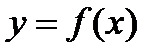 по аргументу xназывается предел отношения приращения функции
по аргументу xназывается предел отношения приращения функции 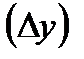 к приращению аргумента
к приращению аргумента 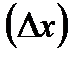 при условии, что
при условии, что 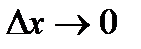 , т.е.
, т.е. 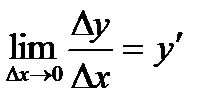 или
или 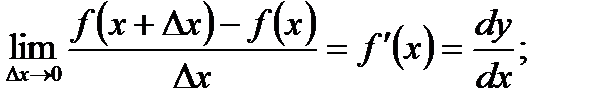
2. 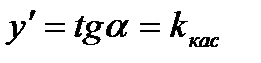 , где a- угол наклона касательной к
, где a- угол наклона касательной к 
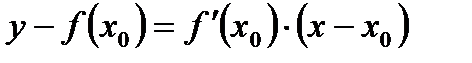 - уравнение касательной, проведённой в т.
- уравнение касательной, проведённой в т. 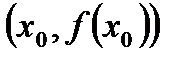
3. 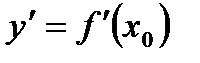 - скорость изменения функции в т. x0.
- скорость изменения функции в т. x0.
- Отыскание производной называется дифференцированием.
-
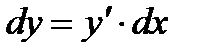 - дифференциал функции равен произведению производной функции на дифференциал аргумента.
- дифференциал функции равен произведению производной функции на дифференциал аргумента.
Геометрически dy представляет собой приращение ординаты касательной к графику функции в заданной точке.
6. 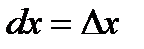 - дифференциал аргумента равен приращению аргумента.
- дифференциал аргумента равен приращению аргумента.
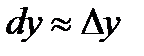 - дифференциал функции и приращение функции равны лишь приближённо.
- дифференциал функции и приращение функции равны лишь приближённо.
7. 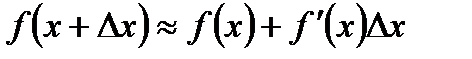 - формуладляприближённыхвычислений.
- формуладляприближённыхвычислений.
Таблица дифференциалов и производных основных элементарных функций.
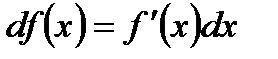
| Элементарные функции | дифференциал | производная |
1. Степенная функция 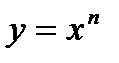 | 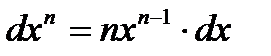 | 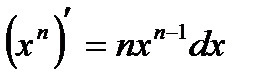 |
2. Линейная функция 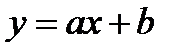 a,b-постоянные y=x. a,b-постоянные y=x. | 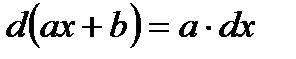 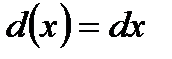 |  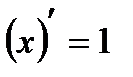 |
| 3.Тригонометрич. функции y=sin x y=cos x y=tg x y=ctg x | 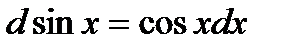 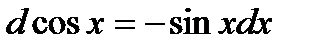 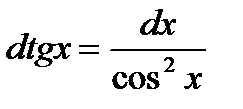 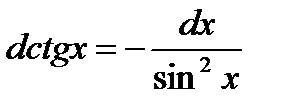 | 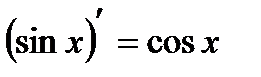 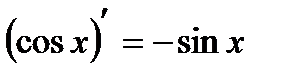 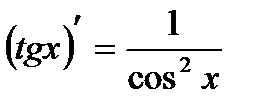 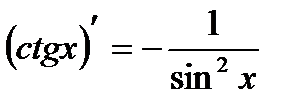 |
4. Показательная функция 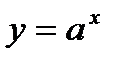 , a -число , a -число 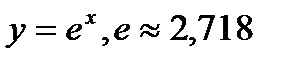 | 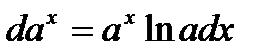 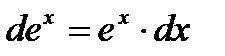 | 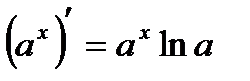 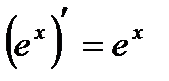 |
5. Логарифмическая функция 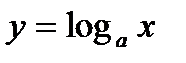 y=ln x y=ln x | 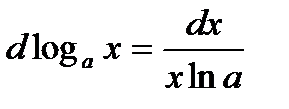 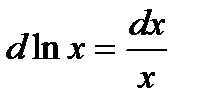 | 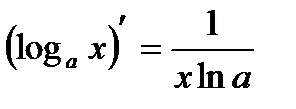 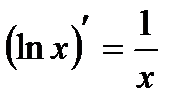 |
6. Иррациональная функция 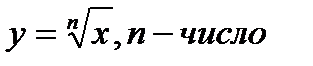 | 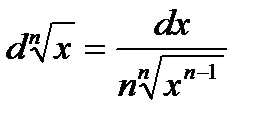 | 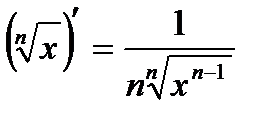 |
| 7. Обратно тригонометричес- кие функции y= arcsin x y=arcos x y= arctg x y=arcctg x | 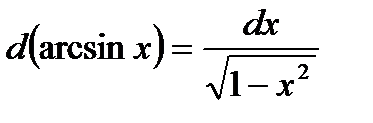 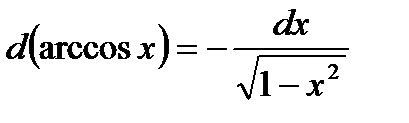 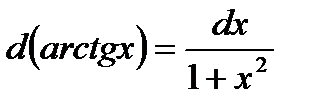 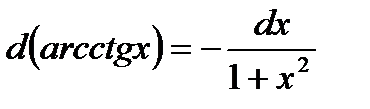 | 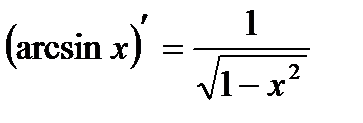 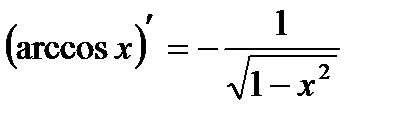 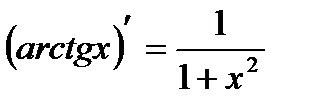 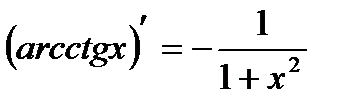 |
| 8. y=c c-const | d(c)=0·dx | 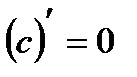 |
Основные правила дифференцирования.
Пусть С- постоянное, 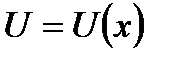 и
и 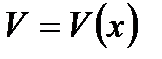 - функции имеющие производные.
- функции имеющие производные.
Тогда:
1) 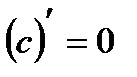
2) 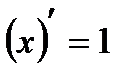
3) 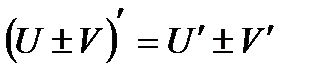
4) 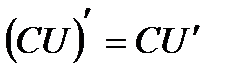
5) 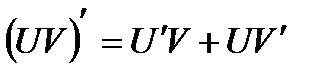
6) 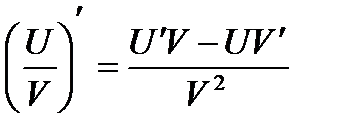
7) если 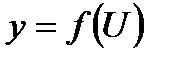 ,
, 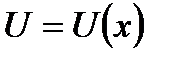 , т.е
, т.е 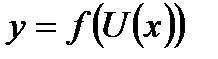 , где функции f(U) и U(x) имеют производные, то
, где функции f(U) и U(x) имеют производные, то 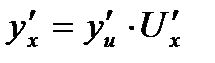 - правило дифференцирования сложной функции.
- правило дифференцирования сложной функции.
5.2 Примеры решения задач.
Задача 1. Найти производные 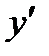 или
или 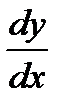 следующих функций:
следующих функций:
а) 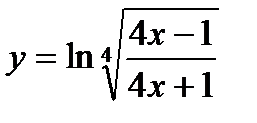
б) 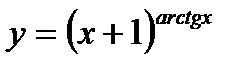
в) 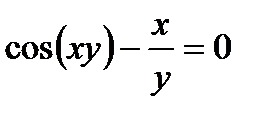
г) 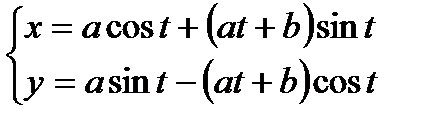
Решение:
а) Пользуясь правилом логарифмирования корня и дроби, преобразуем правую часть:
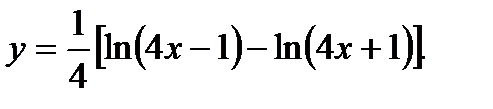
Применяя правила и формулы дифференцирования, получим:
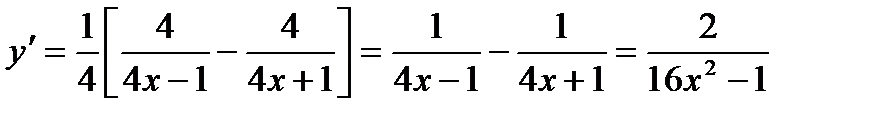
б) Предварительно прологарифмируем по основанию е обе части равенства:
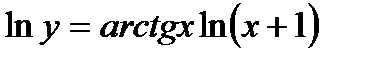
Теперь дифференцируем обе части, считая 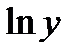 сложной функцией от переменной х:
сложной функцией от переменной х:
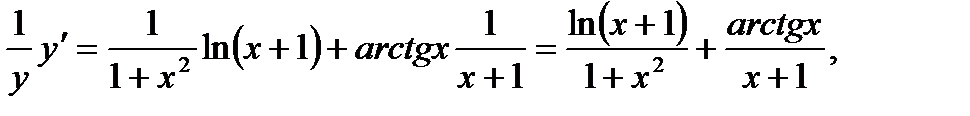
откуда
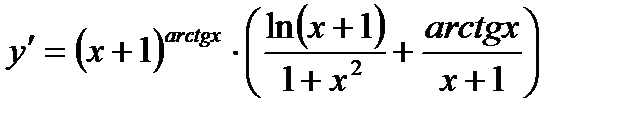
в) В данном случае зависимость между аргументом х и функцией у задана уравнением, которое не разрешено относительно функции у. Чтобы найти производную у', следует дифференцировать по х обе части заданного уравнения, считая при этом у функцией от х, а затем полученное уравнение решить относительно искомой производной у'. Имеем
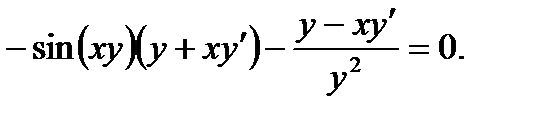
Из полученного равенства, связывающего х, у, и у',
находим производную у':
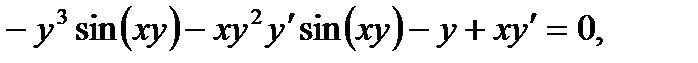
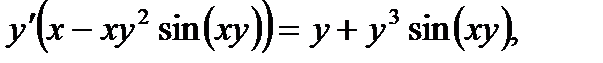
откуда
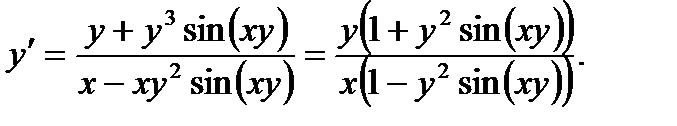
г) Зависимость между переменными х и у задана параметрическими уравнениями. Чтобы найти искомую производную у', находим предварительно дифференциалы dy и dx и затем берем отношение этих дифференциалов
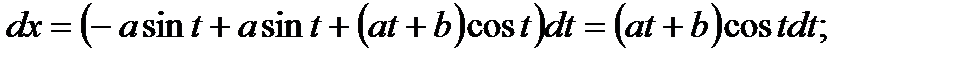
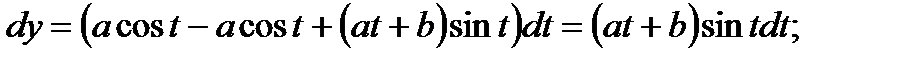
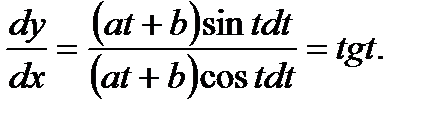
Задача 2. Найти производную второго порядка 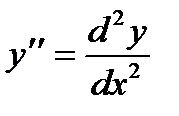
а) 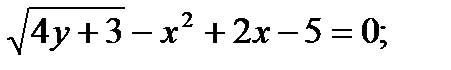
б) 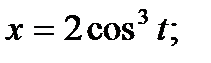
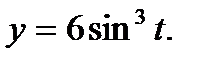
Решение: а) Функция у задана в неявном виде. Дифференцируем по х обе части заданного уравнения, считая при этом у функцией от х:
| (1) |
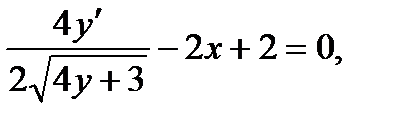
откуда 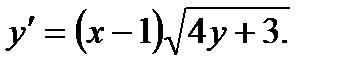
Снова дифференцируем по х обе части (1):
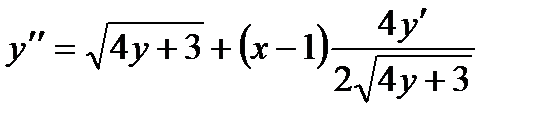 (2)
(2)
Заменив у' в (2) правой частью (1), получим:
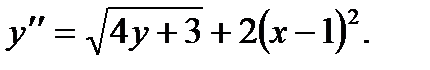
б) Зависимость между переменными xи у задана параметрическими уравнениями. Чтобы найти производную у', находим сперва дифференциалы dy и dx и затем берем отношение этих дифференциалов:
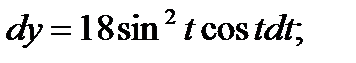
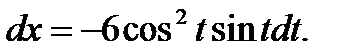
Тогда
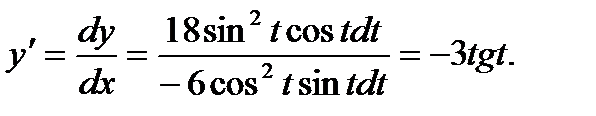
Производная второго порядка 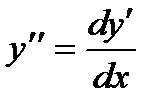 . Следовательно, чтобы найти у", надо найти дифференциал dy':
. Следовательно, чтобы найти у", надо найти дифференциал dy': 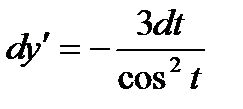
Тогда 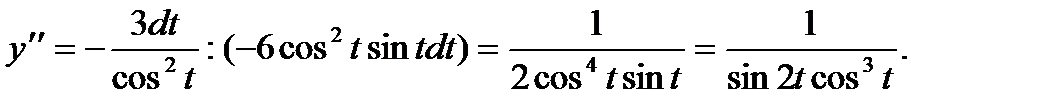
Задача 3. Найти приближенное значение функции 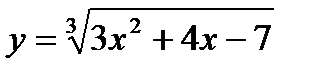 при
при 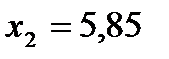 исходя из ее точного значения при
исходя из ее точного значения при 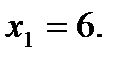
Решение: Известно, что дифференциал dy функции 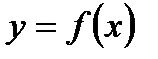 представляет собой главную часть приращения этой функции
представляет собой главную часть приращения этой функции 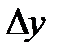 .Если приращение аргумента
.Если приращение аргумента 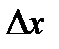 мало по абсолютной величине, то приращение
мало по абсолютной величине, то приращение 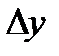 приближенно равно дифференциалу, т. е.
приближенно равно дифференциалу, т. е. 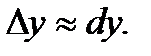 . Так как
. Так как 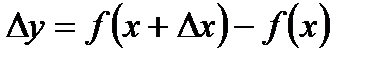 , а
, а 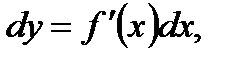 то имеет место приближенное равенство:
то имеет место приближенное равенство:
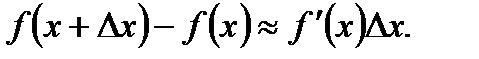
Пусть 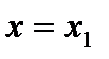 ,
, 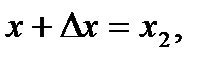 т. е.
т. е. 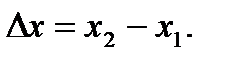
Тогда 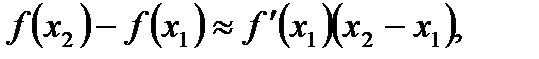
| (1) |
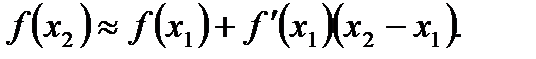
Приближенное равенство (1) дает возможность найти значение функции при 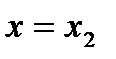 , если известно значение функции и ее производной при
, если известно значение функции и ее производной при 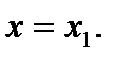 Прежде чем воспользоваться приближенным равенством (1), находим числовое значение производной f'(x) при х= 6:
Прежде чем воспользоваться приближенным равенством (1), находим числовое значение производной f'(x) при х= 6:
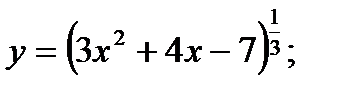
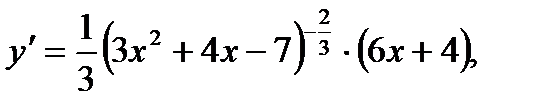 или
или 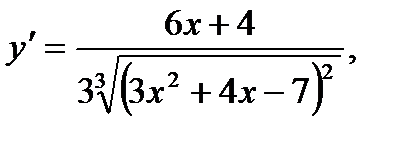
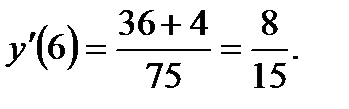
Применяя (1), получаем
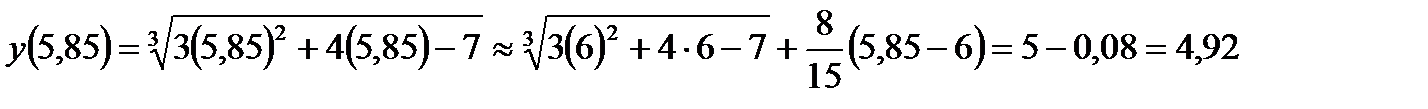
1. Сформулировать определение производной.
2. Каков геометрический смысл производной?
3. Как составить уравнение касательной?
4. Каков геометрический и механический смысл производной?
5. Как найти производную неявной функции? Параметрической функции?
6. Функция непрерывна в т. x0. Следует ли отсюда дифференцируемость функции?
7. В чём заключается геометрический смысл дифференциала функции?
8. Записать формулу, используемую в приближённых вычислениях. Найти приближённое значение 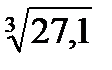
Тема 6. Приложения производной к исследованию поведения функции и построению графика и к другим задачам.
Пискунов, гл. V, §1-12, упр 1-134
Данко, ч. I, гл. 3
План исследования функции и построения графика.
1.Найти область определения функции. Решение этого вопроса указывает на те интервалы оси (ОХ), над которыми пройдёт график и на те значения аргумента x, над которыми график не пройдёт, а также в каких точках пройдут вертикальные асимптоты.
2.Исследовать на чётность, нечётность. Решение этого вопроса облегчает построение.
3.Указать промежутки монотонности функции и найти экстремумы её, точки экстремумов. Построить соответствующие точки на координатной плоскости.
4.Указать точки перегиба графика функции и нанести их на координатную плоскость. Указать промежутки выпуклости, вогнутости.
5.Найти уравнения вертикальных и наклонных асимптот, используя условия для существования этих асимптот. Построить эти линии на координатной плоскости.
6.Найти точки пересечения графика функции с осями координат. Нанести их на плоскость.
7.Исследовать поведение функции на концах области определения. Это поможет при построении графика.
8.Можно взять несколько контрольных точек, в случае уточнения поведения графика.
9.Построить график.
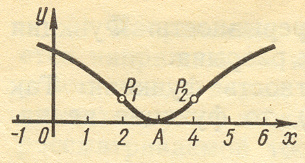
Задача 1. Исследовать функцию у = 1п(х2 — 6х +10) и построить ее график.
Решение:
1. Определим область существования функции. Квадратный трехчлен, стоящий под знаком логарифма, можно представить так: х2— 6x+10=(x-3)2 + 1. Как видно, под знаком логарифма будет положительное число при любом значении аргумента х. Следовательно, областью существования данной функции служит вся числовая ось.
2. Исследуем функцию на непрерывность. Функция всюду непрерывна и не имеет точек разрыва.
3. Установим четность и нечетность функции. Так как у(-х)¹у(х) и у(- х)¹ - у(х), то функция не является ни четной, ни нечетной.
4. Исследуем функцию на экстремум. Находим первую производную:
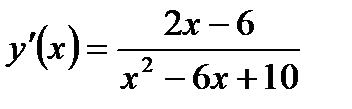
Знаменатель х2- 6x+10>0 для любого значения х. Как видно, при х < 3 первая производная отрицательна, а при х > 3 положительна. При х = 3 первая производная меняет свой знак с минуса на плюс. В этой точке функция имеет минимум:
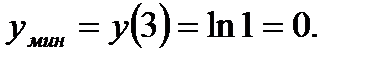
Итак, A(3; 0) - точка минимума. Функция убывает на интервале (- ¥, 3) и возрастает на интервале (3, + ¥).
5. Определим точки перегиба графика функции и интервалы выпуклости и вогнутости кривой. Для этого находим вторую производную:
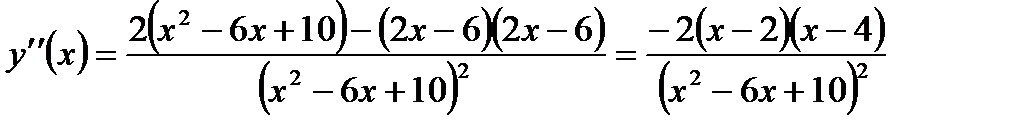
Разобьем всю числовую ось на три интервала: (- ¥, 2), (2, 4), (4, + ¥). Как видно, в первом и третьем интервалах вторая производная отрицательна, а во втором интервале положительна. При x1 = 2 и х2 = 4 вторая производная меняет свой знак. Эти значения аргумента являются абсциссами точек перегиба. Определим ординаты этих точек:
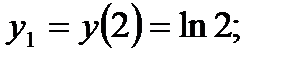
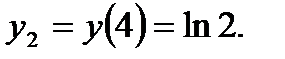
Следовательно, P1 (2; ln 2) и P2(4; ln 2) — точки перегиба графика функции. График является выпуклым в интервалах (- ¥, 2) и (4, +¥) и вогнутым в интервале (2, 4).
6. Определим уравнения асимптот графика функции. Для определения уравнения асимптоты y=kx+b воспользуемся формулами:
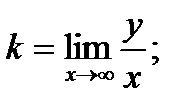
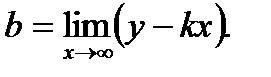
Имеем 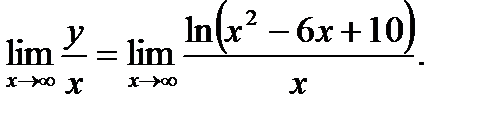
Чтобы найти искомый предел, дважды применяем правило Лопиталя:
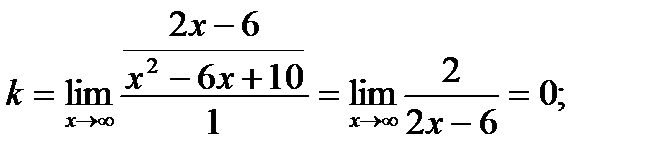
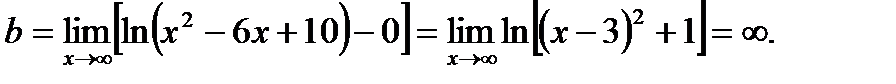
Итак, кривая не имеет асимптот.
 2015-04-20
2015-04-20 3457
3457
