Пискунов, гл X, § 1-14, упр. 1-214.
Данко, гл IX, § 1-5.
7.1 Определение неопределённого интеграла.
Непосредственное интегрирование.
Определение 1. Функция F (x) называется первообразной для функции f (x),
если F´ (x)=f (x) и dF (x)= f (x)dx.
Если функция f (x) имеет первообразную F (x), то она имеет бесчисленное множество первообразных вида F (x)+С, где C- постоянная.
Определение 2. Неопределённым интегралом от функции f (x) или от выражения
f (x)dx называется совокупность всех её первообразных.
Обозначение: 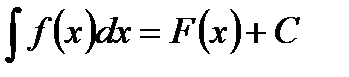
Знак 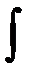 - знак интеграла
- знак интеграла
f (x)- подынтегральная функция
f (x)dx- подынтегральное выражение
x- переменная величина (аргумент функции)
F (x)- первообразная
F(x)+С –совокупность первообразных.
Отыскание неопределённого интеграла называется интегрированием функции.
Таблица неопределённых интегралов.
1. 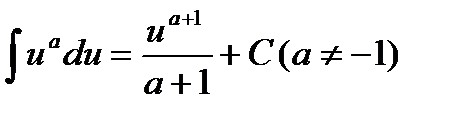
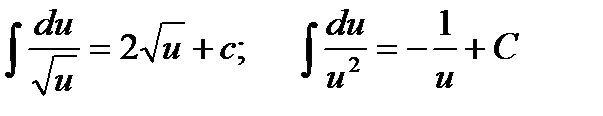
2. 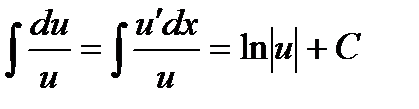
3. 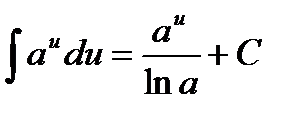
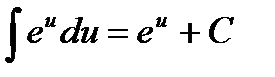
4. 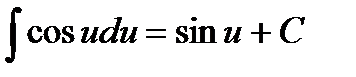 5.
5. 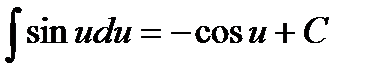
6. 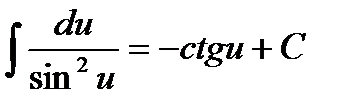 7.
7. 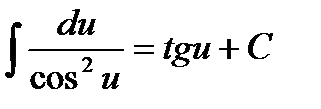
8. 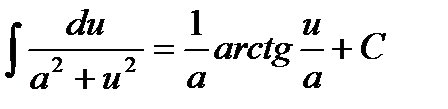
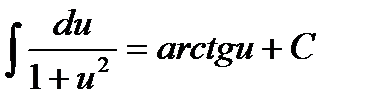
9. 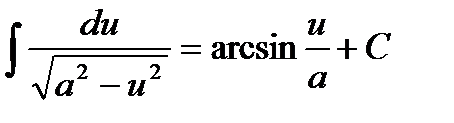
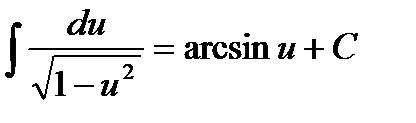
10. 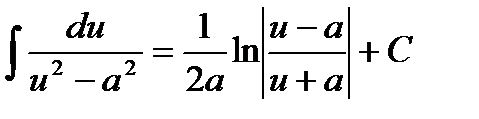
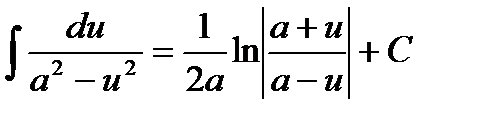
11. 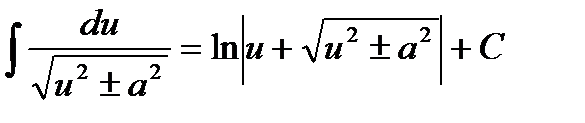 12.
12. 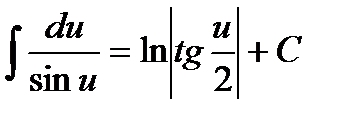
13. 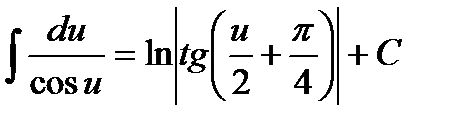 14.
14. 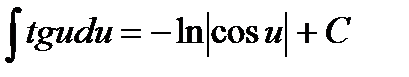
15. 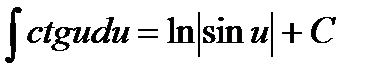 .
.
 2015-04-20
2015-04-20 412
412








