Непараметрические показатели связи. Ранговые коэффициенты связи

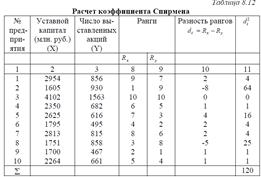
В анализе социальных явлений часто приходится прибегать к различным условным оценкам, например рангам, а взаимосвязь между отдельными признаками измерять с помощью непараметрических коэффициентов связи. Данные коэффициенты исчисляются при условии, что исследуемые признаки подчиняются различным законам распределения.

Ранжирование - это процедура упорядочения объектов изучения, которая выполняется на основе предпочтения.

Ранг - это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической от соответствующих номеров мест, которые определяют. Данные ранги называются связанными.

Принцип нумерации значений исследуемых признаков является основой непараметрических методов изучения взаимосвязи между социальными явлениями и процессами.

К непараметрическим методам исследования можно отнести коэффициент ассоциации К_ас и коэффициент контингенции К_кон, которые используются, если, например, необходимо исследовать тесноту зависимости между качественными признаками, каждый из которых представлен в виде альтернативных признаков.

Для определения этих коэффициентов создается расчетная таблица (таблица «четырех полей»), где статистическое сказуемое схематически представлено в следующем виде:

Признаки	А (да)	А (нет)	Итого
В (да)	a	b	a + b
В (нет)	с	d	c + d
Итого	a + c	b + d	n

Здесь а, b, c, d - частоты взаимного сочетания (комбинации) двух альтернативных признаков 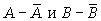; n - общая сумма частот.

Коэффициент ассоциации можно расcчитать по формуле

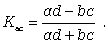(8.11)

Коэффициент контингенции рассчитывается по формуле

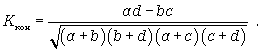(8.12)

Нужно иметь в виду, что для одних и тех же данных коэффициент контингенции (изменяется от -1 до +1) всегда меньше коэффициента ассоциации.

Если необходимо оценить тесноту связи между альтернативными признаками, которые могут принимать любое число вариантов значений, применяется коэффициент взаимной сопряженности Пирсона (К_П).

Для исследования такого рода связи первичную статистическую информацию располагают в форме таблицы:

Признаки	A	B	C	Итого
D	m11	m12	m13	∑m1j
E	m21	m22	m23	∑m2j
F	m31	m32	m33	∑m3j
Итого	∑mj1	∑mj2	∑mj3	П

Здесь m_ij - частоты взаимного сочетания двух атрибутивных признаков; П - число пар наблюдений.

Коэффициент взаимной сопряженности Пирсона определяется по формуле

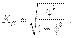(8.13)

где 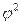- показатель средней квадратической сопряженности:

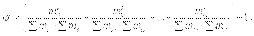
Коэффициент взаимной сопряженности изменяется от 0 до 1.

Наконец, следует упомянуть коэффициент Фехнера, характеризующий элементарную степень тесноты связи, который целесообразно использовать для установления факта наличия связи, когда существует небольшой объем исходной информации. Данный коэффициент определяется по формуле

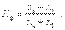(8.14)

где n_a - количество совпадений знаков отклонений индивидуальных величин от их средней арифметической; n_b - соответственно количество несовпадений.

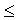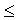Коэффициент Фехнера может изменяться в пределах -1,0 К_ф +1,0.

Коэффициенты, основанные на рангах, позволяют извлечь информацию о направлении связи между признаками, используя понятие коррелируемости на основе подсчета числа пар объектов с взаимно возрастающими, взаимно убывающими и равными значениями признаков.

Коэффициент  Кендалла учитывает число пар с равными признаками и может достигать значений -1 и +1, отражающих высшую степень положительной или отрицательной корреляции между признаками. Обычно вычисляется два варианта статистикиКендалла:  _b и  _c, которые различаются только способом обработки совпадающих рангов.

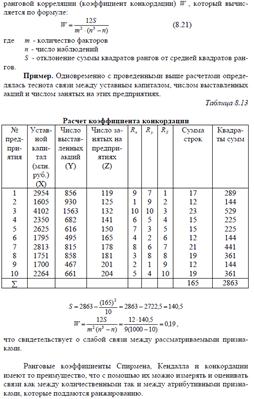
Если в данных имеется много совпадающих значений, предпочтительнее  -статистика Гудмана-Кендалла, которая представляет собой нормированную разность между вероятностью P того, что ранговый порядок двух переменных совпадает, и вероятностью Q того, что он не совпадает:

 = (P - Q)/(P + Q).

Таким образом,  -статистика в основном эквивалентна  Кендалла, за исключением того, что совпадения явно учитываются в нормировке.

Коэффициент d Соммера аналогичен коэффициенту  с дифференциальным учетом пар с равными значениями признаков. Вычисляются два значения коэффициента, учитывающих равенство первого d (A | B), и второго d (B | A) признака.