Категориальная переменная Синонимы: Дискретная переменная. Переменные, принимающие значения из некоторого ограниченного набора категорий. Они обычно связаны с неисчисляемыми признаками, такими как названия (товаров, услуг и др.), имена людей, исходы событий (да/нет) и т.д. Категориальными всегда являются выходные переменные в классификационных моделях (метки классов).
Как правило, значения категориальных переменных являются строковыми. Но иногда могут использоваться и числа, если, например, некоторое наименование кодируется числовым значением. Например, вместо категорий «Низкий», «Средний» и «Высокий» в модели оценки кредитного риска можно использовать значения 0, 1 и 2. Очевидно, что применять обычные математические операции к категориальным переменным нельзя (кроме «равно» - «не равно»), даже если они представлены числами.
Нечисловые статистические данные — это категоризованные данные, вектора разнотипных признаков, бинарные отношения, множества, нечеткие множества и др. Их нельзя складывать и умножать на коэффициенты. Поэтому не имеет смысла говорить о суммах нечисловых статистических данных. Они являются элементами нечисловых математических пространств (множеств). Математический аппарат анализа нечисловых статистических данных основан на использовании расстояний между элементами (а также мер близости, показателей различия) в таких пространствах. С помощью расстояний определяются эмпирические и теоретические средние, доказываются законы больших чисел, строятся непараметрические оценки плотности распределения вероятностей, решаются задачи диагностики и кластерного анализа, и т. д.
Пр.: количество посетителей сайта в течение дня можно отнести к определенным временным отрезкам, например, к часам. Вы легко можете построить соответствующую группировку. Как часто одевают рубашки цвета: зеленого. Желтого и пр. (одномерная таблица: название цвета-частота).
Подаются в таблицах с использованием ранжирования, обеспечивая тем самым и связь между даннми.
Таблицы частот или одновходовые таблицы представляют собой простейший метод анализа категориальных (номинальных) переменных (см. Элементарные понятия статистики). Часто их используют как одну из процедур разведочного анализа, чтобы просмотреть, каким образом различные группы данных распределены в выборке. Например, изучая зрительский интерес к разным видам спорта (с целью рекламы какого-либо продукта на ТВ), вы могли бы представить ответы респондентов следующей таблицей:
| STATISTICA ОСНОВНЫЕ СТАТИСТИКИ | ФУТБОЛ: "Просмотр футбола" | |||
| Категория | Частота | Кумулят. частота | Процент | Кумулят. процент |
| ВСЕГДА: Всегда интересуюсь ОБЫЧНО: Обычно интересуюсь ИНОГДА: Иногда интересуюсь НИКОГДА: Никогда интересуюсь Пропущено | 39 16 26 19 0 | 39 55 81 100 100 | 39.00000 16.00000 26.00000 19.00000 0.00000 | 39.0000 55.0000 81.0000 100.0000 100.0000 |
Таблица показывает частоты, кумулятивные (накопленные) частоты, процент, кумулятивный процент респондентов, выразивших свой интерес к просмотру футбольных матчей в следующей шкале: (1) Всегда интересуюсь, (2) Обычно интересуюсь, (3) Иногда интересуюсь или (4) Никогда не интересуюсь.
Приложения. Практически каждый исследовательский проект начинается с построения таблиц частот. Например, в социологических опросах таблицы частот могут отображать число мужчин и женщин, выразивших симпатию тому или иному политическому деятелю, число респондентов из определенной этнических групп, голосовавших за того или иного кандидата и т.д. Ответы, измеренные в определенной шкале (например, в шкале: интерес к футболу) также можно прекрасно свести в таблицу частот. В медицинских исследованиях табулируют пациентов с определенными симптомами. В маркетинговых исследованиях - покупательский спрос на товары разного типа у разных категорий населения. В промышленности - частоту выхода из строя элементов устройства, приведших к авариям или отказам всего устройства при испытаниях на прочность (например, для определения того, какие детали телевизора действительно надежны после эксплуатации в аварийном режиме при большой температуре, а какие нет). Обычно, если в данных имеются группирующие переменные, то для них всегда вычисляются таблицы частот.
В SPSS имеется большое количество разнообразных процедур, при помощи которых можно произвести анализ связи между двумя переменными. Связь между неметрическими переменными, то есть переменными, относящимися к номинальной шкалу или к порядковой шкале с не очень большим количеством категорий, лучше всего представить в форме таблиц сопряженности. Для этой цели в SPSS реализован тест %2, при котором проверяется, есть ли значимое различие между наблюдаемыми и ожидаемыми частотами. Кроме того, существует возможность расчета различных мер связанности. Восстановление зависимостей между метрическими переменными, то есть имеющими интервальную шкалу или шкалу отношений.
23.Статистические критерии для таблиц сопряженности
Чтобы получить статистические критерии для таблиц сопряженности, щелкните на кнопке Statistics... (Статистика) в диалоговом окне Crosstabs. Откроется диалоговое окно Crosstabs: Statistics (Таблицы сопряженности:Статистика) (см. рис. 11.9).
Флажки в этом диалоговом окне позволяют выбрать один или несколько критериев.
· Тест хи-квадрат (X 2)
· Корреляции
· Меры связанности для переменных, относящихся к номинальной шкале
· Меры связанности для переменных, относящихся к порядковой шкале
· Меры связанности для переменных, относящихся к интервальной шкале
· Коэффициент каппа (к)
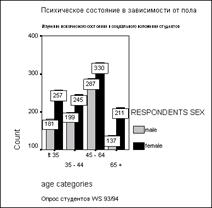
Рис. 11.8: Графическое представление: столбчатая диаграмма
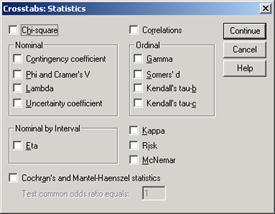
Рис. 11.9: Диалоговое окно Crosstabs: Statistics
· Мера риска
· Тест Мак-Немара
· Статистики Кохрана и Мантеля-Хэнзеля
Эти критерии рассматриваются в двух последующих разделах, причем из-за того, что критерий хи-квадрат имеет большое значение в статистических вычислениях, ему посвящен отдельный раздел.
 2015-04-20
2015-04-20 5566
5566








