ЭДС катушки

Мгновенное значение ЭДС, наведенной в одной катушке с числом витков w_K:

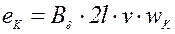(2.7)

Линейная скорость v движения катушки относительно неподвижного магнитного поля

(2.8)

Тогда мгновенное значение ЭДС катушки :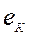

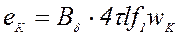(2.9)

ЭДС 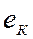в общем случае несинусоидальна, и наряду с первой (основной) гармоникой она содержит ряд высших синусоидальных гармоник.

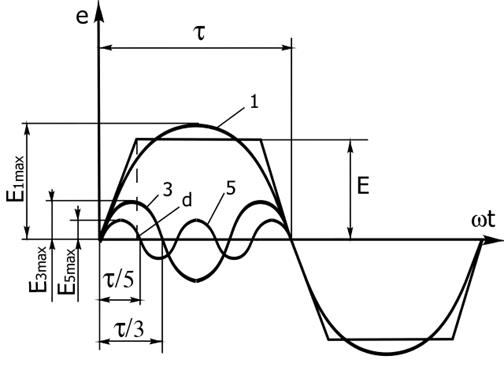
Рис. 2.4. Разложение трапецеидальной кривой ЭДС в гармонический ряд

Если принять форму кривой ЭДС (рис.2.4) трапецеидальной, тогда можно представить ЭДС в виде гармонического ряда

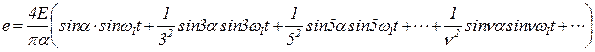, (2.10)

где 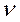- номер гармоники;

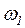- угловая частота основной гармоники.

Известно, что в трехфазных системах при схемах соединения обмоток звездой или треугольником третья гармоника отсутствует. Для исключения пятой гармоники делают укороченным на 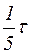шаг обмотки, т.е.:

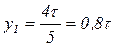
Тогда, в силу того, что амплитуды высших гармоник обратно пропорциональны номеру гармоник, можно считать, что форма кривой индуцированной ЭДС катушки будет практически синусоидальна.

Отношение шага y₁ к полюсному делению τ называют относительным шагом обмотки .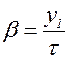

Уменьшение ЭДС катушки при укорочении ее шага на величину относительного укорочения 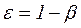учитывается коэффициентом укорочения шага 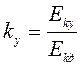, где

Е_kд – действующее значение ЭДС первой гармоники при диаметральном шаге (y₁=τ);

Е_kу - действующее значение ЭДС первой гармоники при укороченном шаге (y₁<τ).

Для первой гармоники:

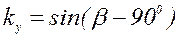(2.11)

Для любой гармоники:

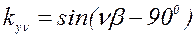(2.12)