| RA | P1 | ||||||||||||
| MA | |||||||||||||
| B | |||||||||||||
| A | a+b+c | ||||||||||||
| Q | |||||||||||||
| ⊕ | |||||||||||||
| ⊖ | M | ||||||||||||
1. Определяем реакции опор.
SMA = MA + P1×(a+b+c) = 0
MA = -P1×(a+b+c) = -45 кН×м
SMB = MA + RA×(a+b+c) = 0
RA = 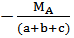 =
= 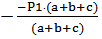 = P1 = 10 кН
= P1 = 10 кН
Проверка: SY = RA - P1 = 0 45-10×4,5 = 0
2. Построим характерный вид эпюр Q и M.
| I уч. | |||||||||||||
| RA | |||||||||||||
| MA | MI | ||||||||||||
| C | |||||||||||||
| A | |||||||||||||
| x | |||||||||||||
| QI |
3. Выполним вычисления и уточним эпюры поперечной силы и изгибающего момента.
|
|
|
SY = RA-QI=0 QI=RA= 10 кН
SMC= MA+RA×x-MI=0 MI= MA+RA×x 0≤x≤(a+b+c)
при x=0,
MI=-45+10×0= -45 кН×м
| ⊕ | Q | ||||||||||||
| -45 | ⊖ | M | |||||||||||
при x=a+b+c=1+1,5+2=4,5 см,
MI=-45+10×4,5= 0
4. Построим эпюры по их аналитическим выражениям.
5. Произведем расчет на прочность балки по допускаемым натяжениям и подберем размеры поперечного сечения.
Mmax = 45 кН×м
При [σ] = 160 МПа, Wx ≥ 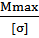 , Wx ≥
, Wx ≥ 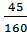
Wx ≥2812,5 см3
Для прямоугольного сечения при m =  = 2,
= 2,
h = 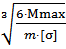 =
= 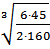 = 20,36 см, b = 40,62 см
= 20,36 см, b = 40,62 см
Для круглого сечения Wx = 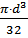 , d =
, d = 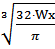 =
=  = 30,598 см ≈ 30,6 см
= 30,598 см ≈ 30,6 см
Для двутавра по таблице сортамента нет решения (Wx Max=2560 см3, №60).
6. Определим перемещения и угол поворота заданного сечения.
yB = 0
yA = = - P1× 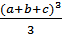 ×
× 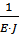 = - 10×103×
= - 10×103× 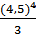 ×
× 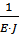 = -
= - 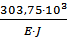
θA = θB =- P1× 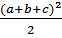 ×
× 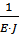 = - 10×103×
= - 10×103× 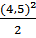 ×
× 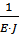 = -
= - 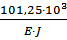
 2015-05-05
2015-05-05 258
258








