1. Последовательность, имеющая предел, ограничена. 2. Последовательность может иметь только один предел. 3. Любая неубывающая (невозрастающая) и ограниченная сверху (снизу) последовательность имеет предел. 4. Предел постоянной равен этой постоянной: 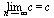
5. Предел суммы равен сумме пределов: 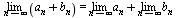 6. Постоянный множитель можно выносить за знак предела:
6. Постоянный множитель можно выносить за знак предела: 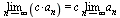
7. Предел произведения равен произведению пределов: 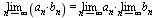 . 8. Предел частного равен частному пределов, если предел делителя отличен от нуля:
. 8. Предел частного равен частному пределов, если предел делителя отличен от нуля: 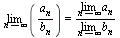
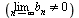 9. Если
9. Если 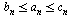 и обе последовательности
и обе последовательности 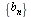 и
и 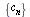 имеют один и тот же предел а, то
имеют один и тот же предел а, то 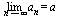
В теоремах 5—8 предполагается, что все пределы в правой части равенств существуют!!!
Пример. Найдем предел 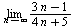 . Имеем
. Имеем 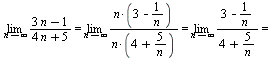
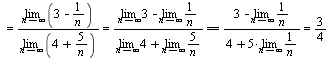
 2015-05-05
2015-05-05 1198
1198








