Современная физика часто оперирует такими понятиями, как радиус атома, расстояние между атомами, длина химической связи и т. п. Техника эксперимента позволяет измерить как размеры атомов всех химических элементов, так и расстояния между атомами в различных реальных структурах. Но прежде чем начать анализ взаиморасположения атомов в кристаллах, следует уточнить физический смысл понятий «радиус атома» и «расстояние между атомами».
Атом не представляет собой классическую корпускулу со строго определенным радиусом. Он состоит из компактного массивного ядра и движущихся вокруг электронов. Ядро имеет массу, составляющую более 99,9% всего атома, но относительно малый размер. Эксперименты по рассеянию ускоренных элементарных частиц на атомных ядрах позволили установить, что радиусы ядер всех стабильных атомов лежат в интервале 10-13 – 10-12 см. Эксперименты по столкновениям атомов газов показали, что электроны атома занимают в пространстве область размером порядка 10-8 см (т. е. порядка одного ангстрема). Для более корректного определения радиуса атома следует принять во внимание, что электроны в атоме не являются классическими материальными точками и их движение невозможно описать непрерывной классической траекторией. Поведение электрона в атоме определяется комплексными волновыми функциями. Эти функции, в принципе, позволяют получить пространственное распределение электрона, точнее, функцию электронной плотности ρ(r) — плотность вероятности нахождения электрона в любой точке пространства. При удалении от атомного ядра на расстояние порядка нескольких ангстрем функция ρ(r) убывает экспоненциально или еще более быстро. Поэтому радиус изолированного атома, строго говоря, понятие условное. Только заранее обговорив, каким малым значением функции р(г) мы будем пренебрегать, мы сможем вычислить конкретное значение радиуса атома.
Для определения радиуса взаимодействующих атомов, находящихся в какой-либо конденсированной структуре, следует вначале однозначно сформулировать понятие межатомного расстояния. Расстояние между атомами целесообразно определить как среднее расстояние между центрами атомов. Центром атома является не просто математическая точка, а месторасположение атомного ядра. Заметим, что определение размеров атомов представляет собой довольно сложную проблему экспериментальной физики. С другой стороны, рентгеноструктурный анализ позволяет с большой точностью определить межатомное расстояние в кристаллах.
При любой температуре атомы совершают тепловые колебания. Частота этих колебаний весьма высока (~1014 c-1), поэтому для геометрического описания структур используются размеры, усредненные по тепловых колебаниям. Межатомное расстояние, измеряемое в экспериментах (рентгеноструктурные исследования, электронная микроскопия, атомная сканирующая микроскопия и т. п.) представляет собой именно усредненное расстояние между центрами атомов.
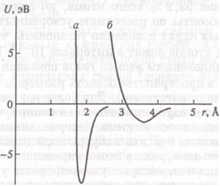
Рис.1. Схематическая зависимость энергии взаимодействия двух атомов от межатомного расстояния: а — сильная связь (ионная, ковалентная, металлическая); б — слабая связь (ван-дер- ваальсова, водородная)
Величина среднего расстояния между атомами определяется межатомным взаимодействием, т. е. типом химической связи. Любое взаимодействие между двумя атомами можно удовлетворительно описать с помощью функции потенциальной энергии U(r), где r — межатомное расстояние. Для изображения графика функции и (r) обычно начало координат совмещается с центром одного атома, а ось Or направляется через центр другого. Аддитивную постоянную потенциальной энергии удобно выбирать из условия и U (r → ∞) → 0. Это значит, что за начало отсчета энергии выбрана суммарная энергия изолированных атомов (рис. 1).
Функции U(r) для пар атомов различных химических элементов обладают индивидуальными особенностями, но все они имеют общие характерные свойства. Если между атомами существует устойчивая химическая связь, то кривая U(r) имеет минимум в отрицательной области значений. Точка минимума r = r0 дает равновесное положение второго атома. Таким образом, величина r0 будет средним межатомным расстоянием d или длиной химической связи (рис.1). При г → 0 каждая функция U(r) неограниченно возрастает. Это означает, что независимо от механизма межатомного взаимодействия (типа химической связи) при сближении атомов возникают силы отталкивания, которые очень резко возрастают при сближении атомов. Расстояние, на котором силы отталкивания становятся преобладающими, определяется перекрыванием волновых функций взаимодействующих электронов.
Когда атом вступает во взаимодействие с другими, т. е. образует химическую связь, то волновые функции его внешних (валентных) электронов претерпевают значительную перестройку. Размер взаимодействующего атома по сравнению с радиусом изолированного может заметно меняется. Экспериментальные исследования структур кристаллов показали, что расстояние d (A, В) между атомами А и В мало зависит от конкретной структуры и, следовательно, и приближенно может служить характеристикой пары атомов данных химических элементов. Сопоставление результатов измерения межатомных расстояний для парных комбинаций атомов разных химических элементов позволяет (в некотором приближении) приписать взаимодействующим атомам определенные эффективные радиусы так, чтобы выполнялось следующее равенство:
d (A, B) = RA + RB. (5.2)
Иначе говоря, межатомное расстояние равно сумме радиусов атомов.
Определенные таким образом радиусы называются кристаллохимическими. С удовлетворительной точностью они обладают свойством аддитивности, т. е. будучи однажды вычисленными, они наблюдаются в новых открываемых или синтезированных кристаллических структурах. Однако величины кристаллохимических радиусов сильно зависят от типа химической связи. Поэтому существует несколько наборов эффективных размеров взаимодействующих атомов, которые сводятся в так называемую систему кристаллохимических радиусов.
Развитием представлений о кристаллохимических радиусах занимались многие кристаллографы и геохимики, начиная с В.Л. Брегга, который дал первую систему кристаллохимических радиусов в 1920 г. Значительный вклад в уточнение и развитие системы радиусов был сделан В. Гольдшмидтом и другими исследователями, составившими различные системы кристаллохимических радиусов. Усовершенствование этих систем продолжается и в наши дни.
В простых веществах атомы объединены ковалентными или металлическими связями. Измерения межатомных расстояний d(AA) в структурах простых веществ позволяет определить так называемые атомные радиусы элементов как половины кратчайших расстояний d(AA):
rат = 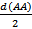
Система атомных радиусов представлена в табл. 1.
Таблица1. Атомные радиусы (в ангстремах) химических элементов
|
| Период | Подгруппа | |||||||
| Ib | IIb | IIIb | IVb | Vb | VIb | Vllb | Vlllb | |
| H 0,46 | He 1,22 | |||||||
| B 0,91 | С 0,77 | N 0,71 | Ne 1,60 | |||||
| A1 1,43 | Si 1,34 | P 1,30 | Ar 1,92 | |||||
| Cu 1,28 | Zn 1,39 | Ga 1,39 | Ge 1,39 | As 1,48 | Se 1,60 | Kr 1,98 | ||
| Ag 1,44 | Cd 1,56 | In 1,66 | Sn 1,58 | Sb 1,61 | Те 1,7 | Xe 2,18 | ||
| Au 1,44 | Hg 1,60 | Tl 1,71 | Pb 1,75 | Bi 1,82 |
Лантаниды и актиниды
|
Во всех периодах таблицы Менделеева наблюдается сходная зависимость атомного радиуса от химического номера элемента. Максимальные значения имеют rат у щелочных металлов. С увеличением числа внешних электронов атомный радиус резко уменьшается, но в конце периода, особенно у инертных газов, вновь возрастает. Рост атомного радиуса с номером периода также имеет место, однако для большинства подгрупп периодической таблицы он не столь ярко выражен. Это означает, что величина rат определяется в большей степени строением внешней электронной оболочки, чем полным числом электронов в атоме.
Ковалентные связи являются направленными, поэтому межатомные расстояния заметно зависят от координационного числа — количества ближайших соседей у каждого атома в данной структуре. Кристаллохимические ковалентные радиусы для тетраэдрической (координационное число 4) и октаэдрической (координационное число 6) координации приведены в табл. 2. Данные таблицы свидетельствуют о том, что для химических элементов 1-й и 2-й групп таблицы Менделеева тетраэдрические радиусы несколько превышают октаэдрические. Для всех остальных элементов, напротив, октаэдрические радиусы заметно превышают тетраэдрические.
Из-за направленного характера ковалентных связей расстояния между одними и теми же атомами в разных соединениях могут несколько отличаться. Особенно сильно зависят межатомные расстояния от кратности связи. Например, для атомов углерода, азота, кислорода и серы сокращение ковалентного радиуса по сравнению с одинарной связью составляют для двойных связей 12-14 %, для тройных — 20-22 %. Для «нецелочисленных» связей длины принимают промежуточные значения.
Таблица 2. Ковалентные октаэдрические радиусы (в ангстремах)
| С 0,97 | N 0,95 | 0,9 | |||
| Mg | A1 | Si | P | S | |
| 1,42 | 1,41 | 1,37 | 1,35 | 1,30 | |
| Cu | Zn | Ca | Ge | As | Se |
| 1,25 | 1,27 | 1,35 | 1,43 | 1,43 | 1,40 |
| Ag | Cd | In | Sn | Sb | Те |
| 1,43 | 1,45 | 1,53 | 1,60 | 1,60 | 1,56 |
| Au | Hg | T1 | Pb | Bi | |
| 1,40 | 1,45 | 1,73 | 1,67 | 1,65 | |
| Mn | |||||
| 1,31 |
Для структур с ионной химической связью используют систему кристаллохимических ионных радиусов, также обладающих свойством аддитивности. В случае ионной связи формируются связующие молекулярные орбитали, заселенные валентными электронами катиона и аниона. Максимум электронной плотности этой орбитали приблизительно совпадает с максимумом электронной плотности атомной орбитали валентных электронов аниона.
| Be 1,07 | В 0,89 | С 0,77 | N 0,70 | 0,66 | |
| Mg | A1 | Si | P | s | |
| 1,46 | 1,26 | 1,17 | 1,10 | 1,04 | |
| Си | Zn | Ca | Ge | As | Se |
| 1,35 | 1,31 | 1,26 | 1,22 | 1,18 | 1,14 |
| Ag | Cd | In | Sn | Sb | Те |
| 1,53 | 1,48 | 1,44 | 1,40 | 1,36 | 1,32 |
| Au | Hg | T1 | Pb | Bi | |
| 1,50 | 1,48 | 1,47 | 1,46 | 1,46 | |
| Mn | |||||
| 1,38 |
 2015-05-05
2015-05-05 2004
2004







