Многослойные плотнейнше упаковки одинаковых шаров

Рассмотрим кратко плотнейшие упаковки, которые могут быть представлены последовательностью слоев (букв) А, В, С с периодом повторяемости, отличным от периода двух- и трехслойных упаковок. Такие упаковки называют обычно n -слойными, понимая под числом n число плотноупакованных слоев, содержащихся в периоде повторяемости. Таким образом, можно записать символы четырехслойной плотнейшей упаковки …| ABAC | ABAC |..., пятислойной …| ABCAB|ABCAB |..., шестислойных

...| ABCACB | ABCACB |... и...| ABABAC | ABABAC |...

и т. д. Кроме числа слоев в периоде повторяемости многослойные плотнейшие упаковки часто называются в соответствии с теми кристаллами, для которых они характерны. Так, четырехслойная упаковка называется также топазовой, шестислойная с символом..,| АВСАСВ | АВСАСВ |... — рамзаитовой и т. д.

На рис.17 схематически показаны схемы чередования плотноупакованных слоев в четырехслойной и шестислойной плотнейших упаковках. 

a б

Рис.17. Схемы чередования плотноупакованных слоев в четырехслойной (а) и шестислойной рамзаитовой (б) плотнейших упаковках:

Выделенные шары определяют тип плотноупакованного слоя. Шары, принадлежащие слоям г, располагаются в точках излома зигзагообразной линии из заштрихованных шаров. Остальные шары принадлежат слоям к

Иногда бывает удобно обозначать плотноупакованные слои в плотнейших упаковках несколько иначе. Как мы уже видели в §4, в плотнейших упаковках каждый плотноупакованный слой (например, А) может лежать или между одинаковыми слоями В, или между слоями С и В. В первом случае мы имеем фрагмент двухслойной упаковки... ВАВ..., во втором — фрагмент трехслойной упаковки... САВ... или... ВАС …. Плотноупакованный слой, который располагается между двумя одинаковыми слоями, обозначается буквой г, а слой, который располагается между разными слоями, буквой к. В этих обозначениях гексагональная плотнейшая упаковка запишется как... гггггг..., кубическая — как... ккккк ….

Группы симметрии n -слойных плотнейших упаковок можно получить следующим образом. Как мы уже видели, один плотноупакованный слой характеризуется двумерной группой симметрии p 6 mm. Группа симметрии двух наложенных друг на друга слоев получается как пересечение двух групп p 6 mm, наложенных таким образом, что оси 3-го порядка одной группы (например, пустот нижнего слоя) совпадают с осями 6-го порядка другой группы (шаров верхнего слоя). Нетрудно убедиться, что в пересечении возникнет группа Р З m. Наложения следующих слоев (шар на пустоту, пустота на шар и т. д.) уже не могут привести к диссимметризации системы. Однако это не означает, что группа симметрии упаковок при различных вариантах построения n -слойных упаковок не будет меняться. Как мы уже видели на примере трехслойной упаковки, может происходить симметризация упаковок. Таким образом, приведенные рассуждения показывают, что пространственные группы симметрии плотнейших упаковок обязательно должны содержать в качестве подгруппы группу Р З m. Просматривая таблицы пространственных групп, можно убедиться, что кроме группы С¹ _{3 v} = Р З m к таким группам относятся пространственные группы C ⁵ _{3 v} = R 3 m, D ³ _{3 d} = P 3 m, D ⁵ _{3 d =} R 3 m, D ¹ _{3 h} = P 6 m 2, C ⁴ _{6 v} = Р 6₃ mc, D ⁴ _{6 h} = P 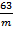mc и O ⁵_h = Fm 3 m.

Установить пространственную группу симметрии каждой конкретной упаковки можно, если использовать ее буквенный символ. При этом можно сформулировать простые правила, которые позволяют найти добавочные по отношению к группе P 3 m элементы симметрии и, тем самым, выбрать одну из перечисленных восьми групп симметрии плотнейших упаковок.

Если буква г разбивает на две зеркально-симметричные части всю бесконечную (г, к) -формулу упаковки, то через этот слой, т. е. через центры шаров слоя, отвечающего символу г, проходит зеркальная плоскость симметрии, перпендикулярная оси 3-го порядка. Это непосредственно следует из того, что оба слоя, соседних со слоем 3, абсолютно идентичны, в том числе инвариантны относительно отражения в указанной плоскости. Аналогично попарно инвариантны относительно данной плоскости и все последующие слои.

Напротив, если символ плотнейшей упаковки рассекается ни две зеркально равные части буквой к, — плоскость симметрии не проходит через этот символ, так как к -слой соседствует с неинвариантными относительно отражения слоями. Однако эти дне части инвариантны относительно центра инверсии, который расположен в слое. Если же всю бесконечную (г, к) -формулу на две зеркально равные части рассекает пара букв кк, то центр инверсии находится между этими слоями.

Этих правил оказывается достаточно, чтобы из восьми возможных пространственных групп плотнейших упаковок выбрать одну, описывающую конкретную плотнейшую упаковку. Рассмотрим н качестве примера одну из двенадцатислойных упаковок и запишем ее (А, В, С) - и (г, к)- формулы:

Символами m и 1 здесь обозначены положения зеркальных плоскостей симметрии и центров инверсии, которые получены в соответствии с приведенными выше правилами. Просматривая восемь групп симметрии плотнейших упаковок, мы увидим, что единственной группой, которая имеет плоскости, перпендикулярные оси 3-го порядка, и центры инверсии, является группа D ⁴ _{6 h} = P 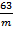mc, которая и описывает симметрию данной двенадцатислойной плотнейшей упаковки.

Заметим, что (г, к) - формула упаковки не позволяет непосредственно определить период идентичности упаковки. В этом легко убедиться на примере той же двенадцатислойной упаковки, где период (г, к) -формулы равен половине периода (А, В, С) -формулы. Из этого следует, что для определения периода идентичности плотнейшей упаковки необходимо записать ее символ в виде (А, В, С) - формулы, период которой полностью соответсвует периоду идентичности рассматриваемой упаковки.

Полный анализ плотнейших упаковок вплоть до п = 12, а также некоторых других можно найти в книге академика Н.В. Белова «Структура ионных кристаллов и металлических фаз» (М.: Изд- во АН СССР, 1947). Мы приведем лишь сводную таблицу, характеризующую упаковки до восьмислойных включительно.

Таблица7. Характеристики многослойных плотнейших упаковок

одинаковых шаров

n	(А, В, С)-формула	(г, к) - формула	Симметрия
	...|AB|AB|...	...|гг|гг|...	Р тс т
	...|ABC|ABC|...	…| ккк | ккк |...	РтЗт
	...|ABAC|ABAC|...	...|кгкг|кгкг|...	Р тс т
	...|ABCAB|ABCAB|...	...|гкккг|гкккг|… \гкккг\гкккг\...	Р3̅т
	...|ABCACB|ABCACB|...	...|гккгкк|гккгкк|… \гккгкк\гккгкк\...	Р тс т
	...|ABABAC|ABABAC|...	...|кгггкг|кгггкг|...	Р6̅т2
	...|ABABACB|ABABACB|…	...|ггггккк|ггггккк|...	Р3̅т
	...|ABCBACB|ABCBACB|...	...|гкгкккк|гкгкккк|...	Р3̅т
	...|ABCBCAC|ABCBCAC|…	...|ккггкгг|ккггкгг|...	Р3̅т
	...|АВСАВАСВ|...	...|гкккгккк|...	Р тс тп
	...|АВАВАСАС|...	...|кгггкггг|...	Р тс т
	...|АВАВАВС|...	...|гггггкгк|...	Р6̅т2
	...|АВАВСАСВ|...	...|гггккгкк|...	Р6̅т2
	...|АВСВСАСВ|...	…|гкггкгкк|...	Р3̅т
	...|АВАСВАСВ|...	...|ггкккккк|...	РЗ̅т