Экспериментальная установка состоит из большого стеклянного баллона 1, соединённого с манометром 2 и насосом.

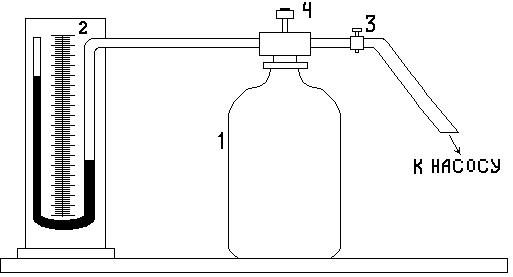 |
рис.1
Кран 3 служит для прекращения выхода воздуха из баллона после накачивания. С помощью клапана с кнопкой 4 внутренний объём баллона может быть на короткое время соединён с атмосферой.
Для измерения давления в данной работе используют жидкостный манометр в виде 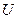 - образной трубки, одно колено соединяется с сосудом, в котором нужно измерить давление, другое колено - открытое. Разность уровней жидкости в коленах называется разностью давления
- образной трубки, одно колено соединяется с сосудом, в котором нужно измерить давление, другое колено - открытое. Разность уровней жидкости в коленах называется разностью давления 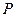 в сосуде и атмосферного давления
в сосуде и атмосферного давления 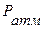 вне его. Таким образом, давление
вне его. Таким образом, давление 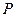 в сосуде больше атмосферного давления на давление жидкости высотой
в сосуде больше атмосферного давления на давление жидкости высотой 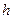 в открытом колене манометра.
в открытом колене манометра.
В манометре, используемом в установке, точность измерений ограничена использованием миллиметровой шкалы (ее основная инструментальная погрешность 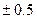 мм.), что обеспечивает незначительную абсолютную погрешность при измерении давления.
мм.), что обеспечивает незначительную абсолютную погрешность при измерении давления.
К систематическим погрешностям измерений следует отнести неточность шкалы, используемой в манометре.
В работе определение 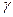 производится классическим методом Клемана – Дезорма, основанным на исследовании некоторого объема воздуха, мысленно выделенного в баллоне.
производится классическим методом Клемана – Дезорма, основанным на исследовании некоторого объема воздуха, мысленно выделенного в баллоне.
Рассмотрим изменения, которые будет претерпевать в процессе опыта некоторый мысленно выделенный объём воздуха в баллоне. С помощью насоса накачаем в баллон некоторое добавочное количество воздуха. При накачивании воздух нагревается. Чтобы начать опыт, нужно подождать несколько минут, чтобы в результате теплообмена температура в баллоне сравнялась с температурой окружающей среды. При этом давление в баллоне несколько снизится.
Рассмотрение процесса начнём с того момента, когда температура и давление в баллоне установились.
 |
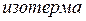 1. Выделенная часть воздуха в баллоне в начале процесса будет характеризоваться параметрами
1. Выделенная часть воздуха в баллоне в начале процесса будет характеризоваться параметрами 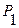 (выше атмосферного),
(выше атмосферного), 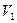 ,
, 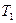
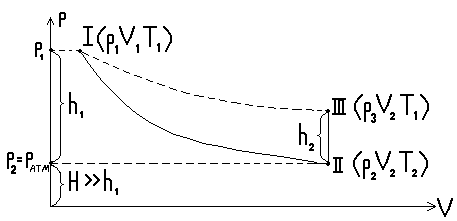
 рис.2
рис.2
(температура окружающей среды), что соответствует точке 1 на диаграмме pV (рис. 2).
2. Произведем адиабатическое расширение воздуха в баллоне. Для этого, нажав кнопку 4, соединим на короткое время внутренний объем баллона с атмосферой. Часть воздуха выйдет из баллона, а выделенный нами воздух расширится. Это расширение можно считать адиабатическим, так как оно происходит быстро и теплообмен с окружающей средой произойти не успевает.
На графике процесс расширения изображен отрезком адиабаты I-II. Давление в баллоне сравнивается с атмосферным, а температура понизится. Параметры выделенной части воздуха примут значение 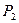 (атмосферное давление),
(атмосферное давление), 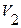 ,
, 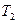 (ниже температуры окружающей среды). Параметры воздуха в начале и в конце расширения связаны уравнением адиабаты (уравнение Пуассона):
(ниже температуры окружающей среды). Параметры воздуха в начале и в конце расширения связаны уравнением адиабаты (уравнение Пуассона):
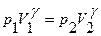 (23)
(23)
3. После адиабатического расширения в течение 2-3 минут произойдет теплообмен между окружающей средой и воздухом в баллоне. Температура в баллоне поднимется до температуры окружающей среды, а давление повысится. Процесс изобразится отрезком изохоры II-III. Параметры газа примут значения P3, V2, T1, (температура окружающей среды).
Сравнивая конечное состояние выделенной части воздуха III с исходным I, можно заметить, что они находятся при одной и той же температуре 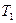 . Такие состояния связаны уравнением изотермы (закон Бойля-Мариотта)
. Такие состояния связаны уравнением изотермы (закон Бойля-Мариотта)
p1 V1 = p3 V2 (24)
Для определения показателя адиабаты возведем уравнение (24) в степень 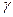 и разделим его почленно на уравнение (23).
и разделим его почленно на уравнение (23).
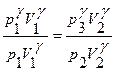 или
или 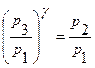 (25)
(25)
Выразим давление воздуха в баллоне через разность уровней жидкости в коленах манометра 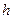 . Обозначим атмосферное давление буквой
. Обозначим атмосферное давление буквой 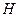 , а добавочное давление в состоянии I буквой
, а добавочное давление в состоянии I буквой 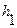 и добавочное давление в состоянии III буквой
и добавочное давление в состоянии III буквой 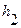 . Тогда
. Тогда 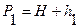 ,
, 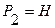 и
и 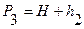 . В результате математических преобразований уравнения (25) получили:
. В результате математических преобразований уравнения (25) получили:
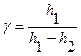 (26)
(26)
Эта формула является рабочей формулой для определения показателя адиабаты g= Cp/Cv,
 2015-05-05
2015-05-05 225
225








