Результаты отдельных экспериментов будут отличаться друг от друга (случайный разброс), что приводит к появлению случайных погрешностей в определении 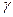 . Исключить случайные погрешности, так же и систематические погрешности, связанные с определением
. Исключить случайные погрешности, так же и систематические погрешности, связанные с определением 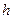 , нельзя. Они должны быть оценены для возможности критического анализа эксперимента. Точность эксперимента оценивают с помощью некоторой средней ошибки.
, нельзя. Они должны быть оценены для возможности критического анализа эксперимента. Точность эксперимента оценивают с помощью некоторой средней ошибки.
В теории вероятностей показывается, что ожидаемое значение такой средней ошибки 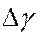 полн. следует вычислять по формуле:
полн. следует вычислять по формуле: 
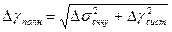 ,
,
где 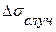 - случайная погрешность;
- случайная погрешность;
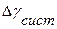 - систематическая ошибка.
- систематическая ошибка.
Затем по формуле: 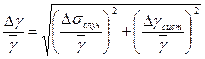 , где
, где 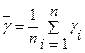 , рассчитывают относительную погрешность в определении
, рассчитывают относительную погрешность в определении 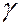 .
.
Рассмотрим вычисление 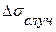 . Вопросами оценки случайных погрешностей занимается теория ошибок. Согласно этой теории, значение случайных погрешностей при большом
. Вопросами оценки случайных погрешностей занимается теория ошибок. Согласно этой теории, значение случайных погрешностей при большом 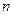 (число измерений) подчиняется статистической закономерности, которая называется законом распределения погрешностей.
(число измерений) подчиняется статистической закономерности, которая называется законом распределения погрешностей.
При определении 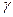 , как показывает эксперимент, таким законом распределения является закон Гаусса (нормальный закон). Согласно этому закону случайные погрешности не должны превышать значения некоторой предельной (случайной) погрешности, которая выражается в виде
, как показывает эксперимент, таким законом распределения является закон Гаусса (нормальный закон). Согласно этому закону случайные погрешности не должны превышать значения некоторой предельной (случайной) погрешности, которая выражается в виде
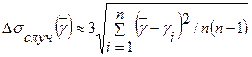 .
.
Случайные погрешности в определении 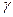 появляются за счет измерения
появляются за счет измерения 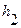 и связаны с тем, что практически невозможно осуществить в каждом опыте точного совпадения длительности открывания баллона со временем адиабатического расширения.
и связаны с тем, что практически невозможно осуществить в каждом опыте точного совпадения длительности открывания баллона со временем адиабатического расширения.
Погрешности в измерении 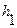 носят систематический характер и определяются ценой деления миллиметровой шкалы.
носят систематический характер и определяются ценой деления миллиметровой шкалы.
Систематическую погрешность находят по правилам отыскания погрешности для косвенных измерений по формуле
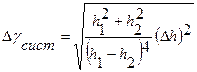 ,
,
где 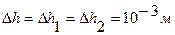 - систематическая погрешность при измерении
- систематическая погрешность при измерении 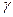 .
.
Пользуясь полученным числовым значением 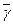 , по формуле (17) оценивают число степеней свободы молекул воздуха.
, по формуле (17) оценивают число степеней свободы молекул воздуха.
 2015-05-05
2015-05-05 246
246








