Если плоская гладкая кривая задана параметрическими уравнениями 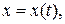
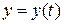 и функции
и функции 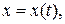
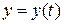 непрерывно дифференцируемы на отрезке
непрерывно дифференцируемы на отрезке 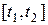 , то длина дуги кривой определяется формулой
, то длина дуги кривой определяется формулой
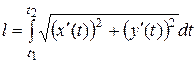 . (2)
. (2)
Пример 4. Найти длину дуги одной арки циклоиды
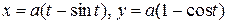 .
.
Какие координаты имеет точка 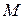 циклоиды, если дуга
циклоиды, если дуга 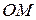 в четыре раза короче длины дуги всей арки? (Рисунок см. в пр.8 следующего раздела).
в четыре раза короче длины дуги всей арки? (Рисунок см. в пр.8 следующего раздела).
Вычислим сначала 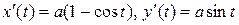 , тогда
, тогда
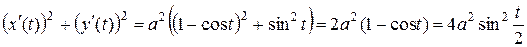 .
.
Мы уже знаем, что для первой арки циклоиды параметр 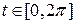 .
.
По формуле (2) находим
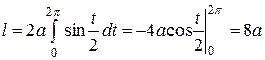 .
.
 Здесь учтено, что
Здесь учтено, что 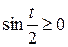 для
для 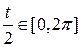 .
.
Значит, длина дуги 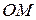 равна
равна 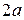 . Найдем, какому значению параметра
. Найдем, какому значению параметра 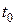 соответствует такая длина. Теперь в соотношении
соответствует такая длина. Теперь в соотношении
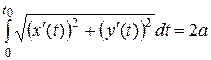
неизвестным является верхний предел интегрирования. Поскольку все необходимые вычисления проделаны выше, запишем

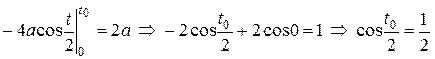 .
.
Решая полученное тригонометрическое уравнение, получаем 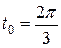 . Осталось вычислить координаты точки
. Осталось вычислить координаты точки 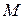 :
:
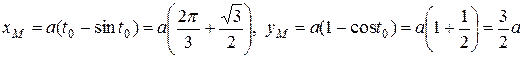 .
.
Пример 5. Найти длину кривой 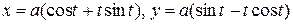 (развертка окружности или эвольвента),
(развертка окружности или эвольвента), 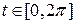 .
.
Вычислим 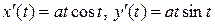 , тогда подынтегральная функция принимает вид
, тогда подынтегральная функция принимает вид 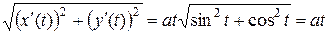 и по формуле (2) находим
и по формуле (2) находим
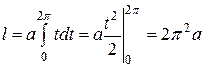 .
.
Длина дуги пространственной кривой, заданной параметрическими уравнениями 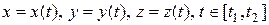 , определяется формулой
, определяется формулой
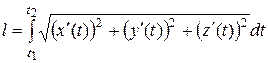 . (3)
. (3)
Пример 6. Найти длину дуги одного витка винтовой линии
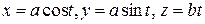 .
.
По формуле (3) при изменении параметра 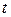 от
от 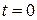 до
до 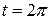 находим
находим
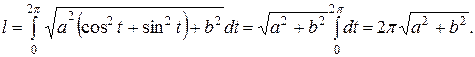
 2015-05-05
2015-05-05 522
522








