a) Формула Ньютона-Лейбница. Пусть функция  непрерывна на отрезке
непрерывна на отрезке 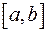 и
и 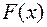 – ее первообразная, тогда
– ее первообразная, тогда
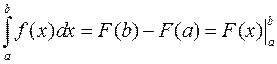 . (1)
. (1)
Пример 1. Вычислить интегралы
a) 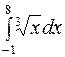 , b)
, b) 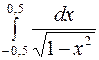 , c)
, c) 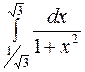 .
.
a) Для функции 
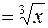 первообразная
первообразная 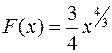 . По формуле Ньютона-Лейбница находим
. По формуле Ньютона-Лейбница находим
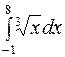 =
= 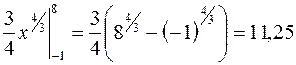 .
.
b) Для функции 
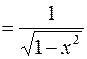 первообразная
первообразная 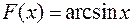 . По формуле (1):
. По формуле (1):
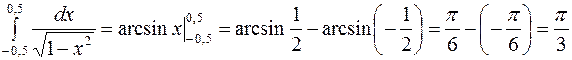 .
.
Для функции 
 первообразная
первообразная 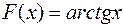 . По формуле (1):
. По формуле (1):
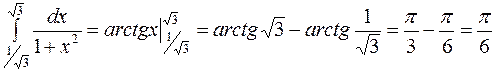 .
.
Пример 2. Вычислить интегралы
a) 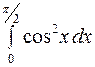 , b)
, b) 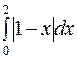 , c)
, c) 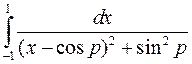 ,
, 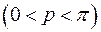 .
.
a) Для вычисления первообразной применим стандартный прием понижения степени: 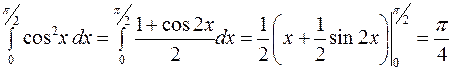 .
.
b) Так как подынтегральная функция 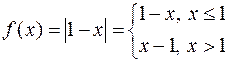 , то следует взять
, то следует взять 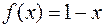 на промежутке интегрирования от
на промежутке интегрирования от 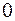 до
до  и
и 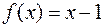 на промежутке от
на промежутке от  до
до 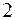 . В силу аддитивности определенного интеграла
. В силу аддитивности определенного интеграла 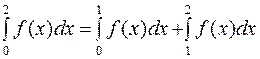 , поэтому
, поэтому
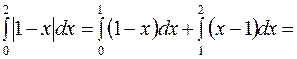
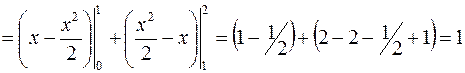 .
.
c) Вычисление первообразной сводится к табличному интегралу 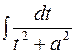 :
: 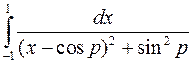 =
= 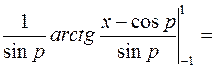
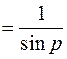
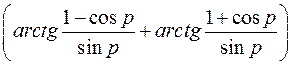 =
= 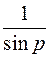
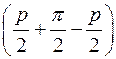 =
= 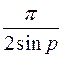 .
.
b) Интегрирование по частям. Пусть функции 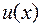 и
и 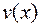 непрерывны вместе со своими производными на отрезке
непрерывны вместе со своими производными на отрезке 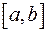 , тогда
, тогда

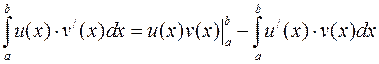
Или 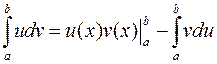 . (2)
. (2)
Пример 3. Вычислить интегралы
a) 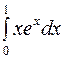 , b)
, b) 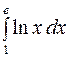 , c)
, c) 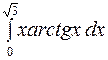 .
.
a) Стандартный для такого интеграла выбор частей и формула (2) приводят к результату:
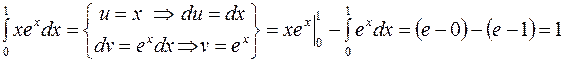 .
.
b) 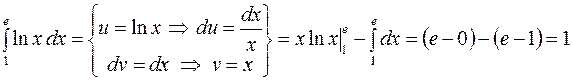 .
.
c) 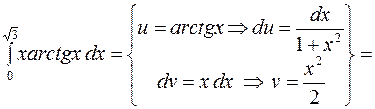
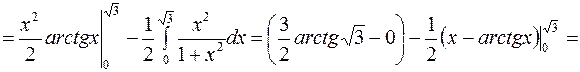
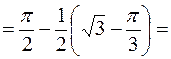
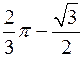 .
.
c) Замена переменной. Пусть выполняются условия:
a) функция  непрерывна на
непрерывна на 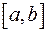 ;
;
b) функция 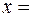
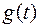 непрерывна вместе со своей производной
непрерывна вместе со своей производной 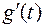 на
на 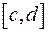 , причем
, причем 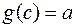 и
и 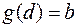 ;
;
с) сложная функция 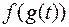 определена и непрерывна на
определена и непрерывна на 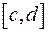 ,
,
тогда
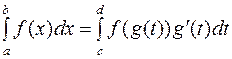 . (3)
. (3)
Пример 4. Вычислить интегралы
a) 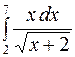 ; b)
; b) 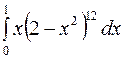 ; c)
; c) 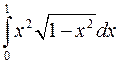 ; d)
; d) 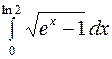 .
.
а) Как и при вычислении неопределенного интеграла, здесь следует рационализировать подынтегральное выражение. Для этого выполним замену переменной 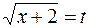 , тогда
, тогда 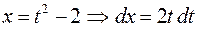 . Но сейчас следует найти пределы изменения новой переменной
. Но сейчас следует найти пределы изменения новой переменной 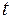 :
:
если 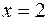 , то
, то 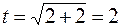 , если
, если 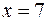 , то
, то 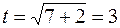 .
.
В соответствии с формулой (3) получаем
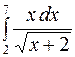
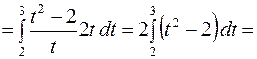
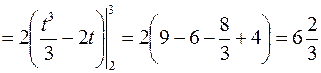 .
.
b) Не стоит возводить двучлен в 12-ую степень и затем интегрировать полином 25—го порядка. Замечая, что 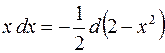 , выполним замену
, выполним замену 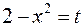 , тогда подынтегральное выражение преобразуется к виду
, тогда подынтегральное выражение преобразуется к виду 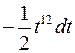 . При изменении
. При изменении 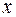 от
от 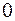 до
до  новая переменная
новая переменная 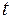 изменяется от
изменяется от 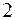 до
до  .
.
По формуле (3) запишем:
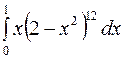
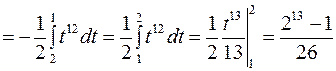 .
.
Здесь учтено свойство определенного интеграла:
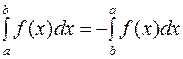 .
.
с) Выполним замену переменной 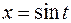 , тогда
, тогда 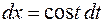 . Найдем пределы изменения новой переменной
. Найдем пределы изменения новой переменной 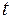 :
:
если 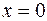 , то
, то 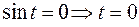 , если
, если 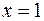 , то
, то 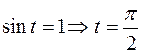 .
.
При этом подынтегральное выражение преобразуется к виду
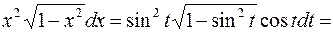
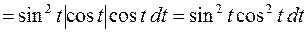 .
.
Здесь учтено, что 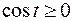 при
при 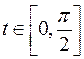 , поэтому
, поэтому 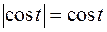 .
.
По формуле (3) найдем
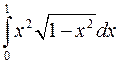 =
= 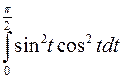 =
= 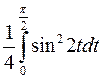 =
= 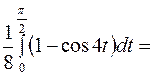
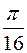 .
.
d) Выполним замену переменной 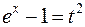 , тогда
, тогда
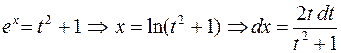 .
.
Найдем пределы изменения новой переменной 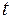 :
:
если 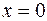 , то
, то 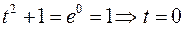 ,
,
если 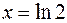 , то
, то 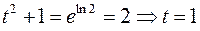 . По формуле (3) получаем:
. По формуле (3) получаем: 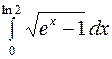
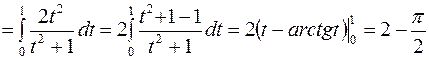 .
.
 2015-05-05
2015-05-05 526
526








