Если гладкая кривая задана уравнением 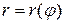 и функция
и функция 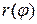 непрерывно дифференцируема на отрезке
непрерывно дифференцируема на отрезке 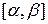 , то длина дуги кривой вычисляется по формуле
, то длина дуги кривой вычисляется по формуле
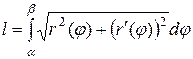 . (4)
. (4)
Пример 7. Найти длину кардиоиды 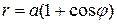 .
.
|
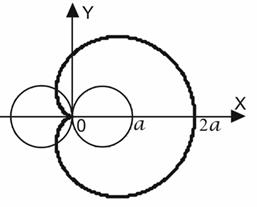
Кардиоиду описывает точка 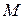 окружности радиуса
окружности радиуса 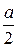 , катящейся без скольжения снаружи по окружности такого же радиуса. Очевидно, полный оборот внешняя окружность делает при
, катящейся без скольжения снаружи по окружности такого же радиуса. Очевидно, полный оборот внешняя окружность делает при 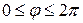 . Симметрия относительно оси абсцисс позволяет взять
. Симметрия относительно оси абсцисс позволяет взять 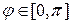 . Вычислим производную
. Вычислим производную 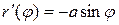 и запишем подынтегральную функцию
и запишем подынтегральную функцию
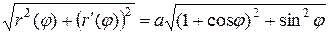
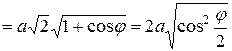 .
.
Теперь по формуле (4) находим
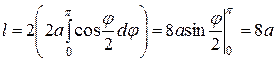 .
.
Здесь учтено, что 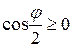 , если
, если 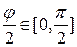 .
.
Пример 8. Найти длину первого витка спирали Архимеда 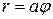 .
.
|
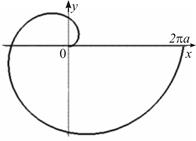
Первый виток спирали соответствует изменению параметра 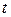 в пределах от
в пределах от 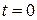 до
до 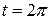 . По формуле (4) запишем
. По формуле (4) запишем
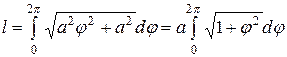 .
.
Интеграл можно вычислить, например, с помощью подстановки 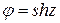 .
.
Мы поступим иначе. Обозначим 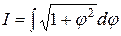 и вспомним метод интегрирования по частям:
и вспомним метод интегрирования по частям:
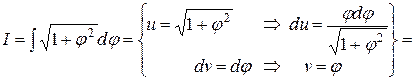
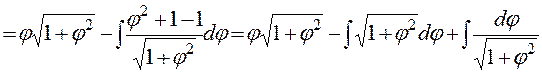 .
.
Так как справа снова получили 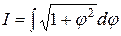 , а табличный интеграл
, а табличный интеграл 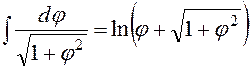 , то пришли к линейному относительно неизвестного интеграла
, то пришли к линейному относительно неизвестного интеграла 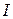 уравнению:
уравнению:


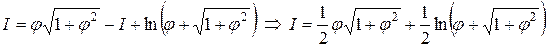 .
.
Значит,
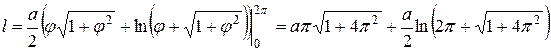 .
.
 2015-05-05
2015-05-05 366
366








