Если гладкая кривая задана уравнением 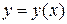 и функция
и функция 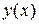 непрерывно дифференцируема на отрезке
непрерывно дифференцируема на отрезке 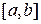 , тодлина дуги этой кривой вычисляется по формуле
, тодлина дуги этой кривой вычисляется по формуле
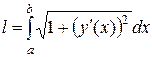 . (1)
. (1)
Пример 1. Найти длину окружности 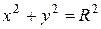 .
.
В силу симметрии кривой достаточно вычислить длину дуги, содержащейся в первой четверти, т.е. 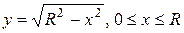 . Найдем сначала производную
. Найдем сначала производную 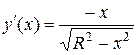 и
и 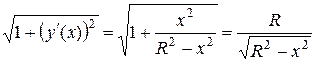 . Теперь по формуле (1) получаем знакомый результат:
. Теперь по формуле (1) получаем знакомый результат:
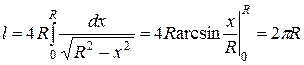 .
.
Пример 2. Найти длину дуги цепной линии 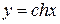 от точки с абсциссой
от точки с абсциссой 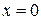 до точки с абсциссой
до точки с абсциссой 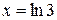 .
.
Найдем сначала 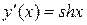 и
и 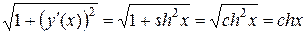 .
.
Здесь учтено основное тождество для гиперболических функций 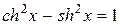 и неравенство
и неравенство 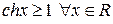 . Значит, по формуле (1) получаем
. Значит, по формуле (1) получаем
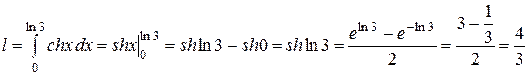 .
.
(Напоминаем, что 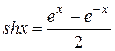 и
и 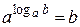 ).
).
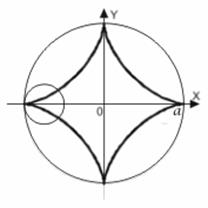
Пример 3. Найти длину дуги астроиды 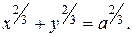
|
Астроиду описывает точка 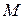 окружности радиуса
окружности радиуса 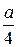 , катящейся без скольжения внутри окружности радиуса
, катящейся без скольжения внутри окружности радиуса 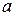 . В силу симметрии астроиды относительно координатных осей достаточно рассмотреть дугу, соответствующую изменению аргумента
. В силу симметрии астроиды относительно координатных осей достаточно рассмотреть дугу, соответствующую изменению аргумента 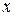 от
от 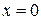 до
до 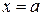 .
.
Сначала вычислим 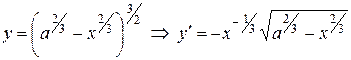 .
.
Значит, подынтегральная функция в формуле (1) имеет вид
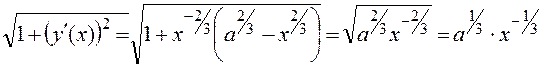 ,
,
а длина дуги астроиды равна 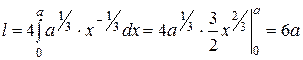 .
.
 2015-05-05
2015-05-05 435
435








