Пусть функция 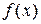 непрерывна на отрезке
непрерывна на отрезке 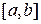 и
и 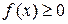 на этом отрезке. Тогда криволинейная трапеция, ограниченная этой кривой, прямыми
на этом отрезке. Тогда криволинейная трапеция, ограниченная этой кривой, прямыми 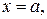
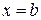 и осью абсцисс, имеет площадь, определяемую формулой
и осью абсцисс, имеет площадь, определяемую формулой
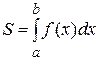 . (1)
. (1)
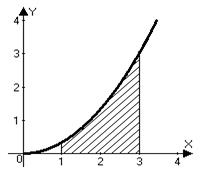 Пример 1. Вычислить площадь криволинейной трапеции, ограниченной параболой
Пример 1. Вычислить площадь криволинейной трапеции, ограниченной параболой 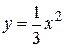 , прямыми
, прямыми 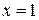 ,
, 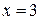 и осью абсцисс.
и осью абсцисс.
По формуле (1) находим
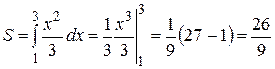 .
.
Пример 2. Вычислить площадь, ограниченную кривой 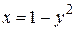 и осью ординат.
и осью ординат.
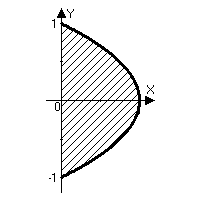 Первый способ. Кривая симметрична относительно оси абсцисс, поэтому достаточно вычислить площадь фигуры, ограниченной осями координат и кривой
Первый способ. Кривая симметрична относительно оси абсцисс, поэтому достаточно вычислить площадь фигуры, ограниченной осями координат и кривой 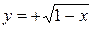 ,
, 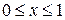 . По формуле (1) находим
. По формуле (1) находим
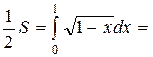
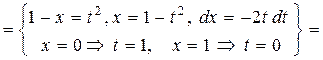
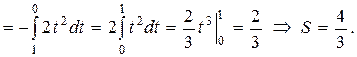
Второй способ. Изменим роли осей координат. Пределы интегрирования по переменной 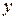 найдём как точки пересечения кривой с осью ординат:
найдём как точки пересечения кривой с осью ординат: 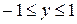 . Тогда (напоминаем о симметрии)
. Тогда (напоминаем о симметрии)
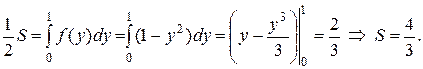
Если 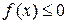 на отрезке
на отрезке 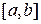 , то
, то
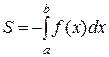 . (2)
. (2)
Пример 3. Найти площадь фигуры, ограниченной синусоидой 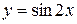 , осью абсцисс и прямыми
, осью абсцисс и прямыми 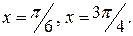
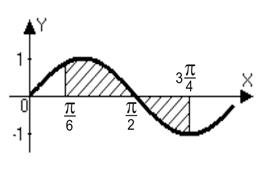 При
При 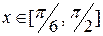 функция
функция 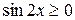 , соответствующую площадь находим по формуле (1):
, соответствующую площадь находим по формуле (1):
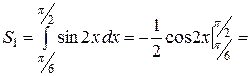
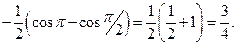
При 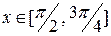 функция
функция 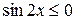 , соответствующую площадь находим по формуле (2):
, соответствующую площадь находим по формуле (2):
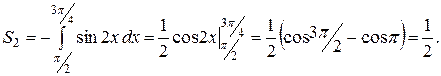
Искомая площадь равна сумме найденных площадей: 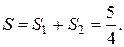
Если плоская фигура ограничена двумя непрерывными кривыми 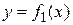 и
и 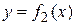 ,
, 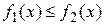 и прямыми
и прямыми 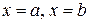 ,
, 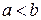 , то её площадь определяется формулой
, то её площадь определяется формулой
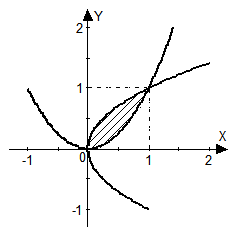
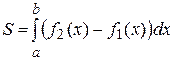 . (3)
. (3)
Пример 4. Найти площадь фигуры, ограниченной параболами 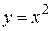 и
и 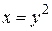 .
.
Точки пересечения парабол найдем, решая систему уравнений

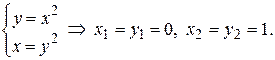
Здесь 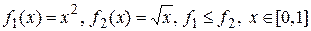
и по формуле (3) находим
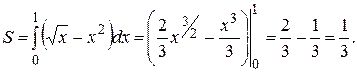
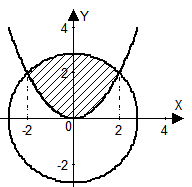 Пример 5. Найти площадь фигуры, ограниченной верхней половиной окружности
Пример 5. Найти площадь фигуры, ограниченной верхней половиной окружности 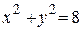 и параболой
и параболой 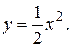
Найдём абсциссы точек пересечения заданных кривых, решая систему уравнений
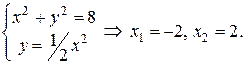
Здесь 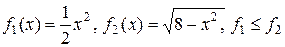 ,
, 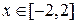 . С учётом симметрии площадь фигуры определяем по формуле (3):
. С учётом симметрии площадь фигуры определяем по формуле (3): 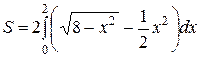 .
.
Вычислим каждый интеграл отдельно:
1. 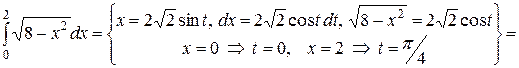
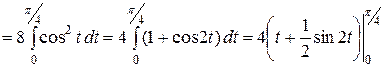 =
= 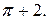
2. 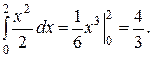
Теперь 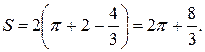
Пример 6. Вычислить площадь фигуры, ограниченной прямой 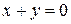 и параболой
и параболой 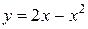 .
.
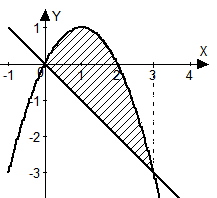 Найдём пределы интегрирования, решая систему
Найдём пределы интегрирования, решая систему
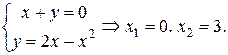
По формуле (3) находим
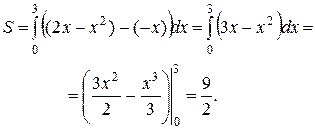
 2015-05-05
2015-05-05 913
913








