2015-05-05
611
Пусть некоторое тело расположено между плоскостям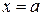и 
и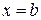 
. Станем рассекать его плоскостями, перпендикулярными оси 
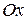. Предположим, что все эти сечения квадрируемы, обозначим 
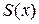- площадь сечения с абсциссой 
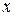и будем считать функцию 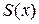непрерывной на 
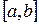. В этих предположениях тело имеет объём, который вычисляется по формуле
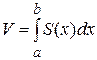. (1)
Действительно, если нарезать тело на элементарные слои толщиной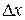 
и каждый слой считать приближенно цилиндром с площадью основания 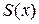и высотой 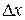, то элементарный объём (объём 
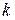-го слоя) равен 
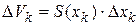, а сумма таких объёмов 
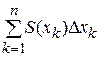есть интегральная сумма для непрерывной (следовательно, интегрируемой) функции .
|
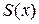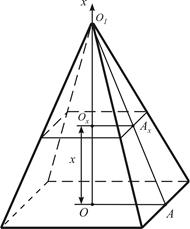
Пример 1. Вычислить объём правильной четырехугольной пирамиды, если высота пирамиды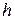 
и сторона основания 
.
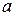Направим ось 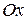от центра основания к вершине пирамиды, тогда 
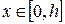. В сечении, проведенном на расстоянии 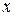от основания пирамиды перпендикулярно оси, получаем квадрат со стороной 
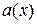, его площадь 
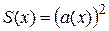. Величину 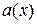найдём из подобия треугольников 
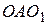и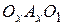 
:
.
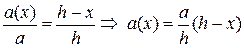Значит,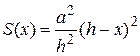 
и по формуле (1) получаем знакомый результат:
.
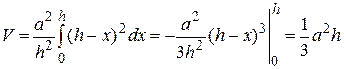Пример 2. Вычислить объём тела, ограниченного трехосным эллипсоидом
.
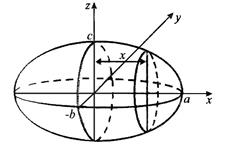
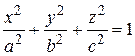На расстоянии 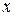от центра эллипсоида в сечении, перпендикулярном оси 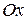, имеем фигуру, ограниченную эллипсом 
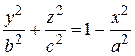, полуоси которого равны
, 
.
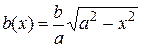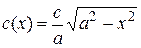Площадь этой фигуры равна (см. замечание к примеру 7 предыдущего раздела)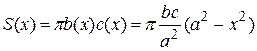 
, 
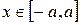. По формуле (1) находим (с учетом симметрии эллипсоида относительно координатной плоскости 
)
.
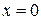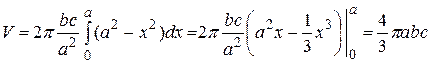Пример 3. Вычислить объём цилиндрического отрезка – тела, отсекаемого от прямого кругового цилиндра плоскостью, проходящей через диаметр основания. В основании цилиндра – круг радиуса :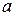 
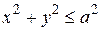, а секущая плоскость проходит через диаметр 
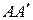и составляет угол 
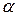с плоскостью основания.
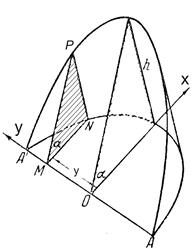Первый способ. В сечении, проведенном на расстоянии 
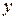от центра круга перпендикулярно оси 
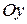, получаем прямоугольный треугольник 
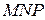с катетами 
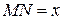и 
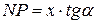, где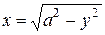 
, 
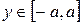. Площадь этого треугольника
.
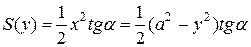По формуле (1) находим (с учетом симметрии тела относительно сечения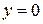 
)
,
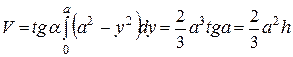где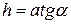 
– высота цилиндрического отрезка.
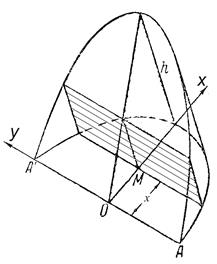Второй способ. В сечении, проведенном на расстоянии 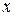от центра круга перпендикулярно оси 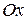, получаем прямоугольник со сторонам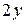и 
и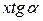 
, здесь 
, 
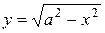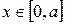. Иначе: если в первом случае мы нарезали тело на треугольные слои перпендикулярно оси 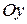, то теперь нарезаем его на прямоугольные слои перпендикулярно оси 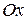. Площадь прямоугольного сечения
,
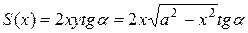а объём тела равен
.
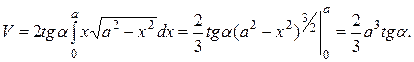Третий способ. Попробуйте самостоятельно получить тот же результат, нарезая тело на тонкие сегменты перпендикулярно вертикальной оси.
