C) Полярные координаты

Если непрерывная кривая задана уравнением 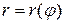в полярных координатах, то площадь сектора, ограниченного этой кривой и полярными радиусам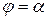и и 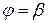, 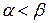вычисляется по формуле

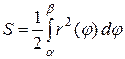. (6)

Пример 9. Найти площадь, заключенную внутри лемнискаты Бернулли

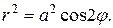
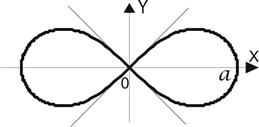Ввиду симметрии фигуры относительно координатных осей достаточно найти четвёртую часть площади (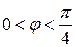). По формуле (6):

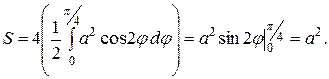
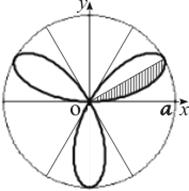
Пример 10. Найти площадь, ограниченную кривой 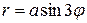(трилистник).

Выясним, где определена данная функция. Условие 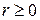приводит к неравенству

,

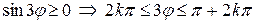откуда 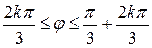. Значит, на плоскости получаем три области (три угла раствором )

,

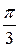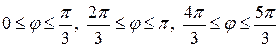в каждой из которых находится один «лепесток».

В силу симметрии достаточно вычислить площадь половины одного лепестка, когда 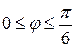. Действительно, при этом полярный радиус увеличивается от 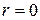до своего максимального значения .

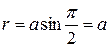По формуле (6) находим:

.

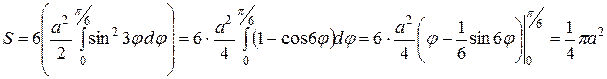Получили четверть площади образующего круга.