I. В ограничениях задачи (1.1) замените знаки неравенств на знаки точных равенств и постройте соответствующие прямые.
II. Найдите и заштрихуйте полуплоскости, разрешенные каждым из ограничений-неравенств задачи (1.1). Для этого подставьте в конкретное неравенство координаты какой-либо точки [например, (0;0)], и проверьте истинность полученного неравенства.
Если неравенство истинное,
то надо заштриховать полуплоскость, содержащую данную точку;
иначе (неравенство ложное) надо заштриховать полуплоскость, не содержащую данную точку.
Поскольку 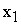 и
и 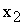 должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси
должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси 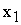 и правее оси
и правее оси 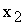 , т.е. в I-м квадранте.
, т.е. в I-м квадранте.
Ограничения-равенства разрешают только те точки, которые лежат на соответствующей прямой, поэтому выделите на графике такие прямые.
III. Определите ОДР как часть плоскости, принадлежащую одновременно всем разрешенным областям, и выделите ее. При отсутствии ОДР задача не имеет решений, о чем сделайте соответствующий вывод.
IV. Если ОДР – не пустое множество, то постройте целевую прямую, т.е. любую из линий уровня 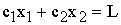 , где L – произвольное число, например, кратное
, где L – произвольное число, например, кратное 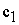 и
и 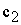 , т.е. удобное для проведения расчетов. Способ построения аналогичен построению прямых ограничений.
, т.е. удобное для проведения расчетов. Способ построения аналогичен построению прямых ограничений.
V. Постройте вектор 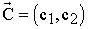 , который начинается в точке (0;0), заканчивается в точке
, который начинается в точке (0;0), заканчивается в точке 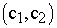 . Если целевая прямая и вектор
. Если целевая прямая и вектор 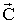 построены верно, то они будут перпендикулярны.
построены верно, то они будут перпендикулярны.
VI. При поиске max ЦФ передвигайте целевую прямую в направлении вектора 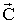 , при поиске min ЦФ – против направления вектора
, при поиске min ЦФ – против направления вектора 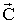 . Последняя по ходу движения вершина ОДР будет точкой max или min ЦФ. Если такой точки (точек) не существует, то сделайте вывод о неограниченности ЦФ на множестве планов сверху (при поиске max) или снизу (при поиске min).
. Последняя по ходу движения вершина ОДР будет точкой max или min ЦФ. Если такой точки (точек) не существует, то сделайте вывод о неограниченности ЦФ на множестве планов сверху (при поиске max) или снизу (при поиске min).
VII. Определите координаты точки max (min) ЦФ 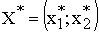 и вычислите значение ЦФ
и вычислите значение ЦФ 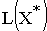 . Для вычисления координат оптимальной точки
. Для вычисления координат оптимальной точки 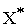 решите систему уравнений прямых, на пересечении которых находится
решите систему уравнений прямых, на пересечении которых находится 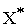 .
.
 2015-05-05
2015-05-05 230
230








