2015-05-05
6883
Пример 1. Материальная точка движется по прямой. Уравнение ее движения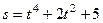 
. Определить мгновенную скорость и ускорение точки в конце второй секунды от начала движения, среднюю скорость и путь, пройденный за это время.
Решение. Мгновенная скорость – это первая производная от пути по времени:
.
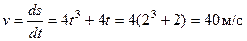Мгновенное ускорение – это первая производная от скорости по времени:
.
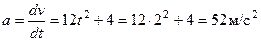Средняя скорость точки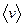 
за время 
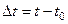определяется по формуле
.
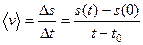Так как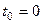 
, то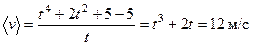 
.
Путь, пройденный точкой за время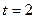 
с, будет равен
.
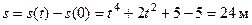Ответ: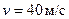 
, 
, 
, 
.
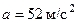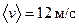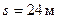Пример 2. Тело движется вниз равноускоренно по наклонной плоскости, и зависимость пройденного пути от времени задается уравнением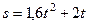 
. Найти коэффициент трения тела о плоскость, если угол наклона плоскости к горизонту равен 30о.
Решение. Коэффициент трения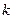 
определяет силу трения при движении тел. Для нахождения 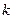рассмотрим, под действием каких сил находится тело. В данном случае на тело действуют силы: сила тяжести 
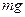, сила реакции опоры 
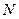и сила трения 
.
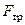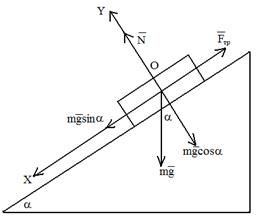
Рисунок 1
Выберем систему координат так, чтобы ось ОХ была параллельна наклонной плоскости (рисунок 1). Тогда согласно второму закону Ньютона, запишем проекции сил на оси:
на OY: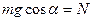 
; на ОХ: 
.
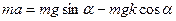Преобразовывая это выражение, можно найти коэффициент трения :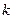
.
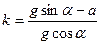Определим величину ускорения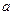 
:
.
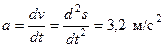Подставив в формулу для 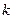численные значения входящих в нее величин, получим коэффициент трения:
.
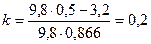Ответ: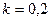 
.
Пример 3. Металлический шарик массой 5 г падает с высоты 1 м на горизонтальную поверхность стола и, отразившись от нее, поднимается на высоту 0,8 м. Определить среднюю силу удара, если соприкосновение шарика со столом длилось 0,01 с.
Решение. Импульс силы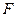 
за время 
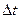, с которым шарик воздействует на поверхность, равен 
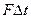. Этот импульс силы будет равен изменению импульса шарика 
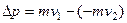, где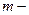 
масса шарика, 
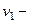скорость, с которой шарик опустился на поверхность стола, 
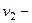скорость, с которой шарик отскочил от поверхности стола. Знак «-» означает, что скорост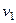и 
и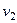 
направлены противоположно.
При свободном падении тела с высоты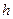 
его скорость на уровне 
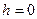определяется по формуле 
.
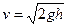Таким образом,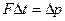 
, 
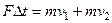, откуда
.
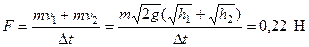Ответ: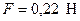 
.
Пример 4. Зависимость угла поворота от времени для точки, лежащей на ободе колоса радиуса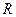 
, задается уравнением 
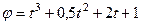. К концу третьей секунды эта точка получила нормальное ускорение, равное 153 м/с2. Определить радиус колеса.
Решение. Для определения радиуса колеса воспользуемся формулой связи нормального ускорения с угловой скоростью:
.
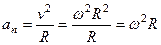Отсюда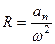 
. Угловую скорость найдем, как первую производную от угла поворота по времени:
.
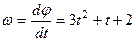Численное значение угловой скорости в конце третьей секунды найдем. Подставив в полученное уравнение дл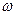я 
время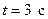 
.
Радиус колеса равен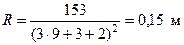 
.
Ответ: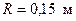 
.
Пример 5. Горизонтальная платформа массой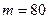 
кг и радиусом 
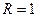м вращается с частотой 
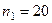об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой 
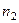будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от 
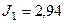до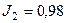 
кг м2? Считать платформу однородным диском.
|
,
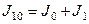а когда человек опустил руки
,
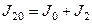где
.
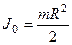По закону сохранения момента импульса
,
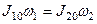где
, 
.
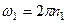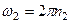Тогда
,
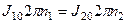откуда
|
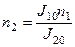. Решая совместно (1) и (2), получим:
,
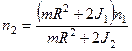откуда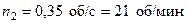 
.
Ответ: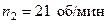 
.
Пример 6. Два свинцовых шарика диаметрами 1 и 2 мм опускают в сосуд с глицерином высотой 0,5 м. Считая, что скорость шариков сразу становится в равномерной, определить, на сколько раньше и какой из шариков достигнет дна сосуда.
Решение. На каждый из шариков, опускающийся в жидкости, действуют три силы – сила тяжести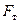 
; сила внутреннего трения (вязкость) 
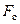, определяемая по формуле Стокса и выталкивающая сила – сила Архимеда 
.
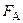Если скорость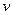 
опускания шариков постоянна, то время опускания 
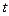будет равно:
.
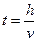Для шариков, опускающихся в глицерин, выполняется условие
.
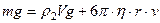Учитывая, что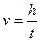 
, получим выражение для :
.
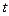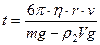Так как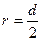 
, 
, 
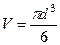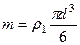, то
.
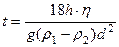Найдем время опускания каждого шарика:
,
.
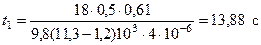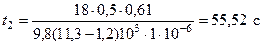Учитывая, что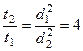 
, делаем вывод, что шарик меньшего диаметра будет опускаться медленнее.
Ответ: шарик большего диаметра достигнет дна сосуда быстрее на 41,64 с.
Пример 7. Ракета движется с большой относительной скоростью. Релятивистское сокращение ее дины составило 15 %. Найти скорость ракеты.
Решение. В системе координат, относительно которой ракета покоится, ее длина равна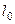 
. В системе координат, относительно которой ракета и связанная с ней система движутся со скоростью 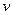, – равна 
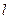. Эти длины связаны соотношением
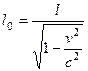, откуда 
.
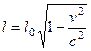По условию задачи:
; 
; 
; 
;
; 
; 
.
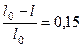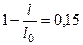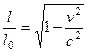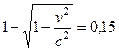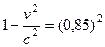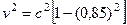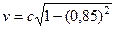Получили, что
.
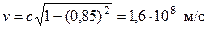Ответ: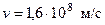 
.
Таблица вариантов
| Номер студента по списку | Номера задач | ||||||
| 1, 11, 21, 31 2, 12, 22, 32 3, 13, 23, 33 4, 14, 24, 34 5, 15, 25, 35 6, 16, 26, 36 7, 17. 27, 37 8, 18, 28, 38 9, 19, 29, 39 10, 20, 30, 40 |
