Распределения Максвелла и Больцмана

Несмотря на то, что скорости всех молекул в процессе хаотического движения непрерывно меняют значения и направления, средняя скорость 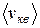остается постоянной при данной температуре (одна из статистических, проявляющихся при наличии большого числа частиц в системе, закономерностей). Это объясняется тем, что в состоянии равновесия реализуется некоторое стационарное распределение молекул по скоростям, подчиняющееся определенному статистическому закону. Этот закон был получен Дж.К. Максвеллом (1831–1879) на основе теории вероятности. Функция (распределения Максвелла молекул по скоростям) f(v) определяет относительное число (долю) молекул dN/N, скорости которых находятся в интервале [ v, v+dv ]:

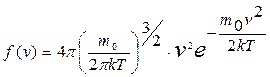. (9.16)

По сути, функция распределения молекул по скоростям f(v) равна вероятности dW встречи в газе молекулы со скоростью, заключенной в интервале [ v,v+dv ]:

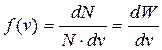. (9.17)

Вероятность же встречи молекулы со скоростью из интервала 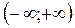– событие достоверное – равна 1, т.е.

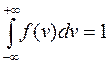. (9.18)

Уравнение (9.18) – условие нормировки.

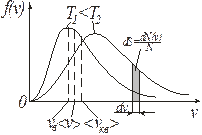
Рис. 9.4

Функция распределения всегда однозначна (вероятность не может иметь несколько значений для данного значения какого-то параметра), конечна (вероятность конечное число).

Подробнее о статистических закономерностях и функциях распределения см. в разделе «Элементы квантовой физики».

Максимум зависимости (и вероятности) f(v) (рис. 9.4) будет соответствовать наиболее вероятному значению скорости v_в. Данное значение можно получить, исследуя уравнение (9.16) на экстремум:

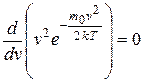, откуда ,

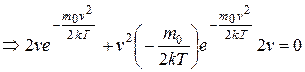что возможно при трех значениях:

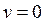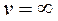, (min функции) и 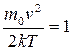(max функции – наиболее вероятная скорость), т.е.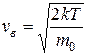

или 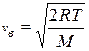. (9.19)

Для получения средней скорости используют методику, принятую в статистической физике: 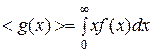. Подставляя x=v, f(x)=f(v) и dx=dv (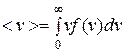) и интегрируя с использованием табличного интеграла

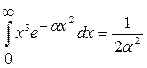, (9.20)

получают среднюю скорость:

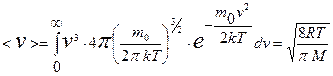. (9.21)

Из формул (9.13), ((9.19) и (9.21) следует, что 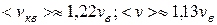(рис. 9.4).

Для получения функции распределения молекул по энергиям (e) необходимо в равенстве 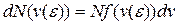(см. 9.20) провести, исходя из уравнения 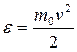, замены .

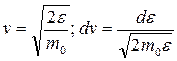Тогда

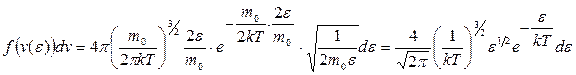
и 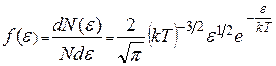. (9.25)

Находя среднее значение энергии аналогично (9.21), получают (9.1): .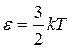

До сих пор считалось распределение молекул в пространстве равномерным. Однако в действительности это не так, поскольку молекулы газа всегда находятся в поле внешних сил, например, в поле тяготения. Силы тяготения удерживают атмосферу у поверхности земли, не давая ей рассеяться вследствие теплового движения в окружающем пространстве. В результате устанавливается некоторое стационарное распределение молекул, при котором давление и концентрация молекул (плотность) убывают с ростом высоты (атмосфера разрежается).

Найдем зависимости P=f(h) и n=f(h) в предположении однородного поля тяготения и постоянства температуры.

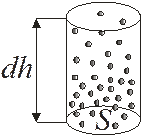
Рис. 9.5

Из уравнения Менделеева – Клапейрона

, .

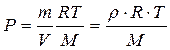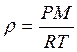Разность давлений на верхнее и нижнее основание мысленно выделенного цилиндра (рис. 9.5) равна весу столба воздуха, приходящемуся на единицу S основания, т.е. гидростатическому давлению P столбика dh:

.

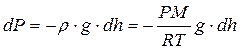Знак «–» показывает, что давление убывает с ростом высоты. Разделяя в данном дифференциальном уравнении переменные 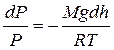и интегрируя 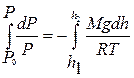, получают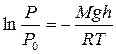

или 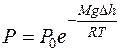(9.23)

Уравнение (9.23) – барометрическая формула Л.Больцмана (1844–1906 гг.).

Так как по условию рассмотрения T=const, то из формулы (9.23) с учетом равенства (9.12) получают зависимость n=f(h) для концентрации:

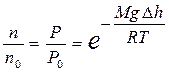Þ 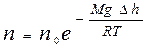. (9.24)

Распределение (9.24) можно переписать в другом виде с учетом равенств 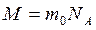и :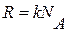

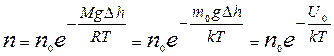, (9.25)

где U ₀ – потенциальная энергия молекулы во внешнем силовом поле (тяготения).