Определение. Дифференциальное уравнение 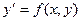 называется уравнением с разделяющимися переменными, если его можно записать в виде
называется уравнением с разделяющимися переменными, если его можно записать в виде
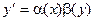 .
.
Такое уравнение можно представить также в виде:
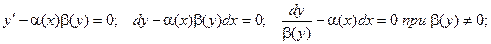
Перейдем к новым обозначениям 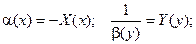
Получаем: 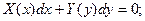
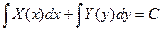
После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.
Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение.
Пример. Найти общее решение дифференциального уравнения: 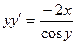
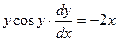
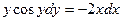
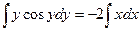
Интеграл, стоящий в левой части, берется по частям:
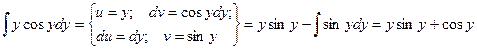

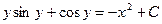
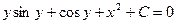
- это есть общий интеграл исходного дифференциального уравнения, т.к. искомая функция и не выражена через независимую переменную. В этом и заключается отличие общего (частного) интеграла от общего (частного) решения.
Чтобы проверить правильность полученного ответа продифференцируем его по переменной х.
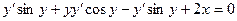
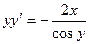 - верно
- верно
Пример. Найти решение дифференциального уравнения 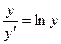 при условии у(2) = 1.
при условии у(2) = 1.
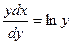
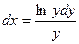
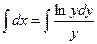
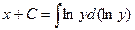
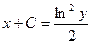
при у(2) = 1 получаем 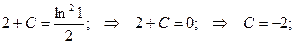
Итого: 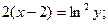 или
или 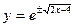 - частное решение;
- частное решение;
Проверка: 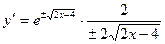 , итого
, итого
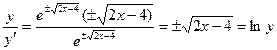 - верно.
- верно.
Пример. Решить уравнение 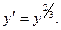
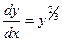
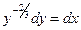
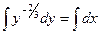
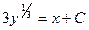
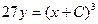 - общий интеграл
- общий интеграл
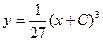 - общее решение
- общее решение
Пример. Решить уравнение 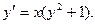
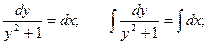
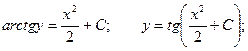
Пример. Решить уравнение 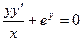 при условии у(1) = 0.
при условии у(1) = 0.
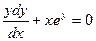
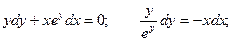

Интеграл, стоящий в левой части будем брать по частям.
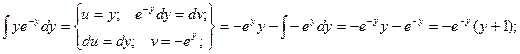
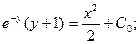
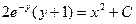
Если у(1) = 0, то 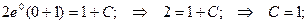
Итого, частный интеграл: 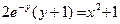 .
.
Пример. Решить уравнение 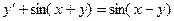 .
.
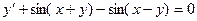
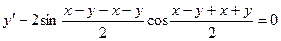
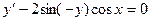
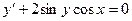
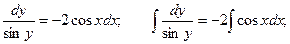
Для нахождения интеграла, стоящего в левой части уравнения см. Таблица основных интегралов. Получаем общий интеграл:
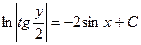
Пример. Решить уравнение 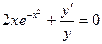
Преобразуем заданное уравнение:
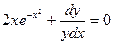
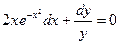
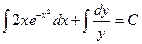
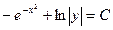
 Получили общий интеграл данного дифференциального уравнения. Если из этого соотношения выразить искомую функцию у, то получим общее решение.
Получили общий интеграл данного дифференциального уравнения. Если из этого соотношения выразить искомую функцию у, то получим общее решение.
Пример. Решить уравнение 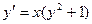 .
.
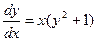
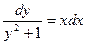
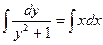 ;
; 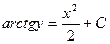 ;
;
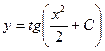
Допустим, заданы некоторые начальные условия х0 и у0. Тогда:
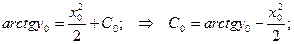
Получаем частное решение 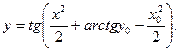
Однородные уравнения.
Определение. Функция f(x, y) называется однородной n – го измерения относительно своих аргументов х и у, если для любого значения параметра t (кроме нуля) выполняется тождество:
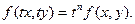
Пример. Является ли однородной функция 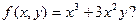
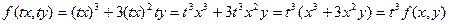
Таким образом, функция f(x, y) является однородной 3- го порядка.
Определение. Дифференциальное уравнение вида 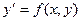 называется однородным, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов.
называется однородным, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов.
Любое уравнение вида 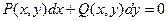 является однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового измерения.
является однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового измерения.
Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными.
Рассмотрим однородное уравнение 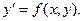
Т.к. функция f(x, y) – однородная нулевого измерения, то можно записать:
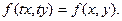
Т.к. параметр t вообще говоря произвольный, предположим, что 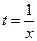 . Получаем:
. Получаем:
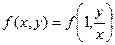
Правая часть полученного равенства зависит фактически только от одного аргумента 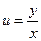 , т.е.
, т.е.
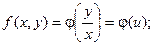
Исходное дифференциальное уравнение таким образом можно записать в виде:
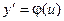
Далее заменяем y = ux, 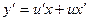 .
.
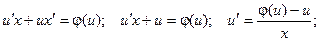
таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u.
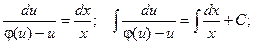
Далее, заменив вспомогательную функцию u на ее выражение через х и у и найдя интегралы, получим общее решение однородного дифференциального уравнения.
Пример. Решить уравнение 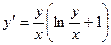 .
.
Введем вспомогательную функцию u.
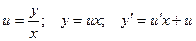 .
.
Отметим, что введенная нами функция u всегда положительна, т.к. в противном случае теряет смысл исходное дифференциальное уравнение, содержащее 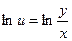 .
.
Подставляем в исходное уравнение:
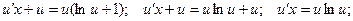
Разделяем переменные: 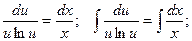
Интегрируя, получаем: 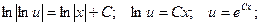
Переходя от вспомогательной функции обратно к функции у, получаем общее решение:
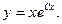
 2015-05-05
2015-05-05 276
276








