2015-04-20
5703
Призмой называется многогранник, состоящий из двух плоских многоугольников, лежащих в разных плоскостях и совмещающихся параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников (рис.38)
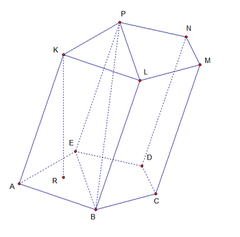 Рис.38 KLMNP, ABCDE – основания призмы, АК, ЕР, СМ, … - ребра, KR - высота Свойства призмы 1. Основания призмы равны и параллельны. 2. Боковые ребра равны и параллельны. 3. Боковые грани — параллелограммы Различают прямыеи наклонные призмы |
Прямая призма - это призма, у которой боковые ребра перпендикулярны основаниям (рис.39)
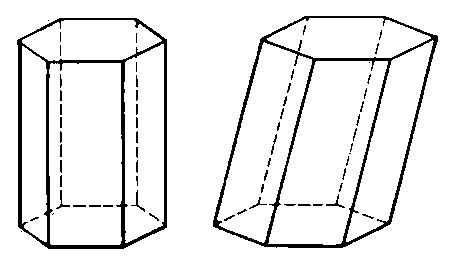
Рис.39
Высота прямой призмы равна боковому ребру.
H = AA1 =…
Боковые грани прямой призмы — прямоугольники.
ABB1A1 — прямоугольник, BCC1B1 — прямоугольник,...
Наклонная призма - это призма, у которой боковые ребра не перпендикулярны плоскостям оснований (рис.40)
Рис.40
Правильная призма — прямая призма, в основании которой лежит правильный многоугольник. У такой призмы все боковые грани — равные прямоугольники. У такой призмы все боковые грани — равные прямоугольники.
По виду основания призмы различают треугольные, четырехугольные, п -угольные призмы.
Треугольная, четырехугольная,..., n-угольная призма — в основании призмы лежит треугольник, четырехугольник,..., n-угольник (рис.41)
| треугольная | четырехугольная | Пятиугольная | шестиугольная |
 |  |  |  |
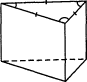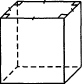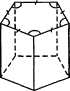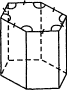Рис.41
Параллелепипедом называется призма, в основании которой лежит параллелограмм (рис.42)
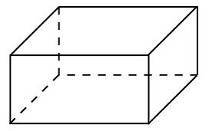
Рис.42
