Так как хорда АВ основания конуса стягивает дугу в 60°, то она равна радиусу основания: АВ = ОА = ОВ (рис. 69). Проведем 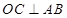 и соединим отрезком точки С и М. Тогда
и соединим отрезком точки С и М. Тогда 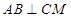 (по теореме о трех перпендикулярах) и угол МСО — линейный угол двугранного угла с ребром АВ. По условию, МСО = 45°.
(по теореме о трех перпендикулярах) и угол МСО — линейный угол двугранного угла с ребром АВ. По условию, МСО = 45°.
В задаче спрашивается площадь сечения, то есть площадь треугольника MAB. 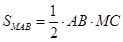 .
.
Найдем сначала OC. Так как треугольник MOC равнобедренный, то OC=OM=10. Тогда гипотенуза 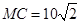 .
.
Рассмотрим ∆COB – прямоугольный, 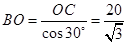 .
. 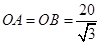 .
.
Подставим числа в формулу: 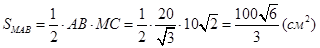 .
.
Ответ: 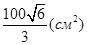 .
.
 2015-04-20
2015-04-20 2122
2122








