Формула Фейнмана-Каца

Этот билет идет в конспекте после билета (22). Вообще, надо поставить общую задачу Коши и разобраться с распределениями Лапласа...

Теорема:

Пусть 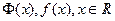- непрерывные функции, 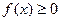, 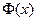- ограничена Þ

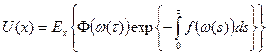
является единственным ограниченным решением диф.уравнения второго порядка

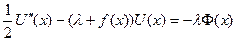
где t - экспоненциально распределенный момент остановки, не зависящий от бр. движения w.

ОПР: функция называется кусочно-непрерывной, если $ конечное число разрывов I рода.

(Разрыв I рода - это наиболее простой разрыв непрерывности функции, при котором $-ют конечные определенные пределы как слева 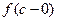, так и справа 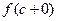. Значение функции в самой точке 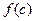будет, вообще говоря, отличным от 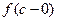и )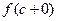

Теорема:

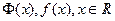- кусочно-непрерывные функции, 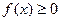, 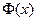- ограничена Þ

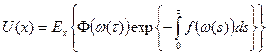
является единственным ограниченным решением диф.уравнения второго порядка

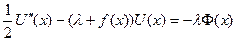
Замечание: Уравнение с кусочно-непрерывными коэффициентами следует понимать как обычное уравнение во всех точках непрерывности, а в точках разрыва решение полагается непрерывным вместе с первой производной.