Опр. Функция у= f (x) называется дифференцируемой в точке х0, если ее приращение в х0 можно представить в виде ∆у=А∆х+α(∆х)∆х (*), где А – некоторое число, α(∆х) – функция от ∆х, являющаяся бесконечно малой при ∆х→0. Связь между дифференцируемостью функции в точке и существованием производной в этой же точке устанавливает Теорема.
Теорема. Для того чтобы f (x) была дифференцируема в точке х0, необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Доказательство. 1. Необходимость. Пусть функция у= f (x) дифференцируема в х0. Тогда ее приращение можно представить в виде (*). Следовательно
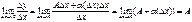
Следовательно производная существует и равна А. 2. Достаточность. пусть существует конечная производная f ′ (х0)=А. Тогда по определению производной, lim∆х→0(∆у/∆х)=А. положим, что α(0)=0 и α(∆х)= (∆у/∆х) – А, если ∆х≠0. Определеннная так функция α(∆х) является бесконечно малой при ∆х→0. Действительно lim∆х→0α (∆х)= lim∆х→0((∆у/∆х) – А)=А – А=0. Кроме того, ∆у=А∆х+α(∆х)∆х. Тем самым доказано, что функция дифференцируема в х0.
Замечание. Если функция дифференцируема в х0, то из (*) следует, что ∆у→0, когда ∆х→0, т.е. функция непрерывна в данной точке. Обратное утверждение неверно. Функция может быть непрерывной, но не дифференцируемой в данной точке.
Пусть f (x) дифференцируема в х0,следовательно, существует производная и коэффициент А из (*) совпадает с производной, как следует из доказательства теоремы. Тогда формулу (*) можно представить
f (x)=f(х0)+ f ′ (х0) ∆х +α(∆х)∆х. α(∆х) б.м. функция (∆х→0)
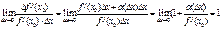
(**)
∆f(х0)~ f ′ (х0) ∆х (приращение функции эквивалентно произведению производной на приращение аргумента)
 2015-05-05
2015-05-05 1859
1859
