По коо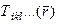рдинатам точки пространства

Пусть – тензорное поле r ^го ранга. Каждую из 3 ^r компонент этого поля продифференцируем по каждой из трех координат x ₁, x ₂, x ₃. Получим совокупность 3 ^{r +1} функций вида 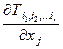(j = 1, 2, 3).

Тº. Если 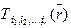– тензорное поле ранга r, то 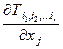будет тензорным полем ранга (r + 1).

◀ Отметим что, если x_i = p_{ii ¢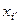} то 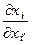= p_{ii ¢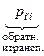} = , и следовательно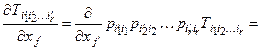

▶

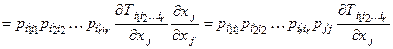Итак, дифференцирование тензорного поля по координатам повышает ранг тензорного поля на единицу.

В частности, применение этой операции к скалярному полю φ порождает векторное поле 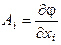, которое называется градиентом скалярного поля.

По аналогии с градиентом скалярного поля, тензорное поле 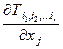(j = 1, 2, 3 ) называют градиентом тензорного поля ранга r.

§15. Дифференциальные операции 1^го порядка

1°. Для векторного поля A_i образуем градиент векторного поля 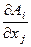, а затем получившийся тензор свернем по индексам i, j: .

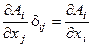Как известно, такая величина в векторном анализе называется дивергенцией векторного поля А (div A). Подобным образом можно получить дивергенцию тензорного поля любого ранга, выше нулевого.

Результирующее тензорное поле имеет ранг на единицу меньший, чем исходное поле.

Для тензорного поля ранга r можно получить r различных тензорных полей (r – 1)^го ранга типа «дивергенции» в зависимости от того, какой из индексов исходного поля сворачивается с индексом дифференцирования: .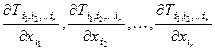

2°. В векторном анализе известна такая дифференциальная операция, как rot A = Ñ´ A. В тензорном представлении 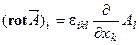. Оператором 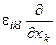можно действовать на тензор любого ранга выше нулевого и затем сворачивать индекс l с одним из индексов этого тензора. Результирующее тензорное поле имеет тот же ранг, что и исходное.

Для тензорного поля ранга r можно получить r различных тензорных полей r ^го ранга типа «ротор» в зависимости от того с каким из индексов исходного поля сворачивать индекс l.

.

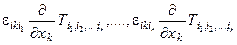3°. Схематически операции градиента, дивергенции и ротора тензорного поля произвольного ранга можно задать следующим образом:

(grad T …) _i = ,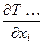

(div T … _i …) = ,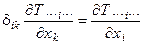

(rot T … _l …) = .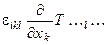

§16. Дифференциальные операции 2^го порядка

1°. Для скалярной функции φ: 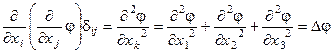, и такая величина называется лапласианом функции.

Аналогично можно ввести лапласиан произвольного тензора ранга r и получить тензорное поле того же ранга: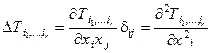

Рассмотрим divrot A, где А – произвольное векторное поле:

Div rot A =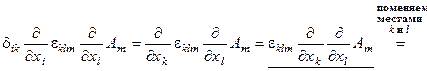

.

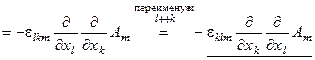Равенство подчеркнутых выражений позволяет заключить, что divrot A = 0 для любого векторного поля А.

Аналогичное тождество имеет место для тензорного поля любого ранга (кроме нулевого): .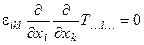

3°. Проверим справедливость тождества: rot rot 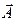= grad div 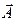- Δ .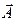

◀ (rot rot A) _i =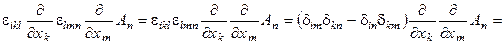

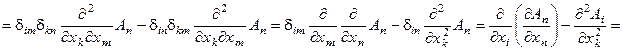
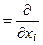(div A) - (D A) _i = (grad div A) _i - (D A) _i = (grad div A - D A) _i ▶

Аналогичное тождество можно записать и для произвольного тензорного поля.