Псевдотензоры

В аналитической геометрии при рассмотрении 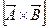направление результирующего вектора устанавливается условно в зависимости от выбора системы координат. В физике такая ситуация встречается при определении направления векторов угловой скорости, момента сил и др..

В то же время направление таких векторов, как скорость, ускорение, сила определяется физическим смыслом и не зависит от выбора системы координат.

В свете этого:

Для ортогональных преобразований: ,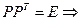

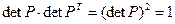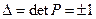
Поэтому все линейные ортогональные преобразования разбиваются на два класса: класс собственных линейных ортогональных преобразований, для которых 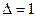(непрерывные преобразования) и класс несобственных линейных ортогональных преобразований, для которых Δ = –1 (преобразования отражения).

В зависимости от закона преобразования компонент по отношению к этим классам линейных ортогональных преобразований все тензорные величины можно разделить на истинные тензоры (или просто тензоры) и псевдотензоры.

Def: Псевдотензоры – это величины компоненты, которых преобразуются по закону: .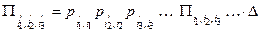

Напомним, что для истинного тензора закон преобразования имеет вид:

.

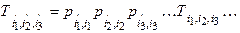Из законов преобразования тензоров и псевдотензоров легко убедиться, что:

1°. Сумма двух псевдотензоров – псевдотензор.

2°. Произведение двух псевдотензоров – истинный тензор.

3°. Произведение псевдотензора на истинный тензор – псевдотензор.

4°. Свертка псевдотензора дает псевдотензор низшего ранга.

Примеры: 1) Если 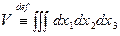, то =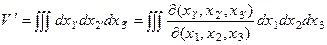

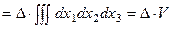, т.е. V¢ = D× V, где D = ±1.

Таким образом, V согласно определению, есть псевдотензор нулевого ранга, т.е. псевдоскаляр.

2) Символ Кронекера d _ik представляет собой единичный, симметричный, инвариантный относительно ортогонального преобразования системы координат, истинный тензор 2^го ранга.

3) В паространстве Е ₃ в фиксированной системе координат К с ортами е ₁, е ₂, е ₃ рассмотрим величины e _ikl = (e_i ´ e_k) e_l.

Ясно, что в правой системе координат: e₁₂₃ = e₂₃₁ = e₃₁₂ = 1; e₂₁₃ = e₁₃₂ = e₃₂₁ = –1. Остальные e _ikl равны нулю.

Рассмотрим, как преобразуются величины e _ikl при линейных ортогональных преобразованиях. Перейдем в систему К¢ с ортами е _1¢, е _2¢, е _3¢:

e _{i ¢ k ¢ l ¢} = (e_{i ¢}´ e_{k ¢}) e_{l ¢} = (р_{i ¢ i} e_i ´ р_{k ¢ k} e_k) р_{l ¢ l} e_l = р_{i ¢ i} р_{k ¢ k} р_{l ¢ l} (e_i ´ e_k) e_l.

Если k и k ¢ – обе правые (или левые), то e _ikl = (e_i ´ e_k) e_l. Если k и k ¢ разной ориентации, то: –e _ikl = (e_i ´ e_k) e_l . Тогда: e _{i ¢ k ¢ l ¢} = р_{i ¢ i} р_{k ¢ k} р_{l ¢ l} e _ikl ×D (D = ±1, в зависимости от того рассматривается собственное или несобственное преобразование)

По определению величины e _ikl образуют псевдотензор 3^го ранга. Он называется алгебраическим символом Леви-Чивита и образует единичный абсолютно антисимметричный псевдотензор 3^го ранга, инвариантный относительно любого ортогонального преобразования координат.

Легко видеть, что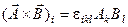

4) Непосредственным вычислением можно убедиться, что 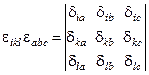, свертка

по индексам l и c дает: 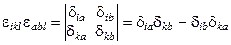, свертка еще по двум индексам k и b дает: e _ikl e _akl = 2d _ia, и наконец полная свертка приводит к: e _ikl e _abc = 6.

5) С помощью символа Леви-Чивита легко получить, например, известную формулу для двойного векторного произведения трех векторов:

{ A ´(B ´ C)} _i = e _iklA_k (B ´ C) _l =e _iklA_k e _lmnB_mC_n = e _ikl e _lmnA_kB_mC_n = (d _im d _kn - d _in d _km) A_kB_mC_n =

= d _im d _knA_kB_mC_n - d _in d _kmA_kB_mC_n = d _imA_nB_mC_n - d _inA_mB_mC_n = B_iA_nC_n - C_iA_mB_m = B_i (A × C) - C_i (A × B) = { B (A × C) - C (A × B)} _i.

§12. Связь тензоров 2^го ранга с матрицей линейного